Math Arguments

Reworking Pythagoras

Pythagorean theorem: \(a^2 +b^2 = c^2\)

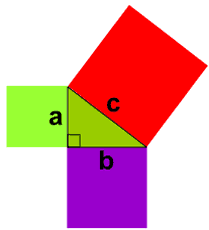
“In a right triangle, the area of the square drawn on the hypotenuse is equal to the sum of the areas of the squares drawn on the other two legs.”

Here is the problem: does the figure whose areas we compare, drawn on the triangle's legs, have to be square?

Can there be other shapes – triangles, rhombuses, regular pentagons, etc. – that make the Pythagorean Theorem more generally true?

.