11 of 11 Items .... Course:
Problems, Questions, and Puzzles to spark discussion and argument in the maths classroom.
. . . View This Fullsize
The Beauty of Mathematics
Is this a thing?
Will it continue?
How will it continue if it does continue?
Can you show why it works?
Does something interesting happen in a prime base like Base-7 or Base-13?
.: [], [Twitter], [New].
. . . View This Fullsize
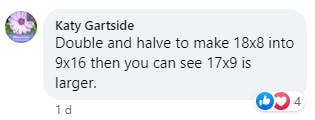
Let's pose a question ...
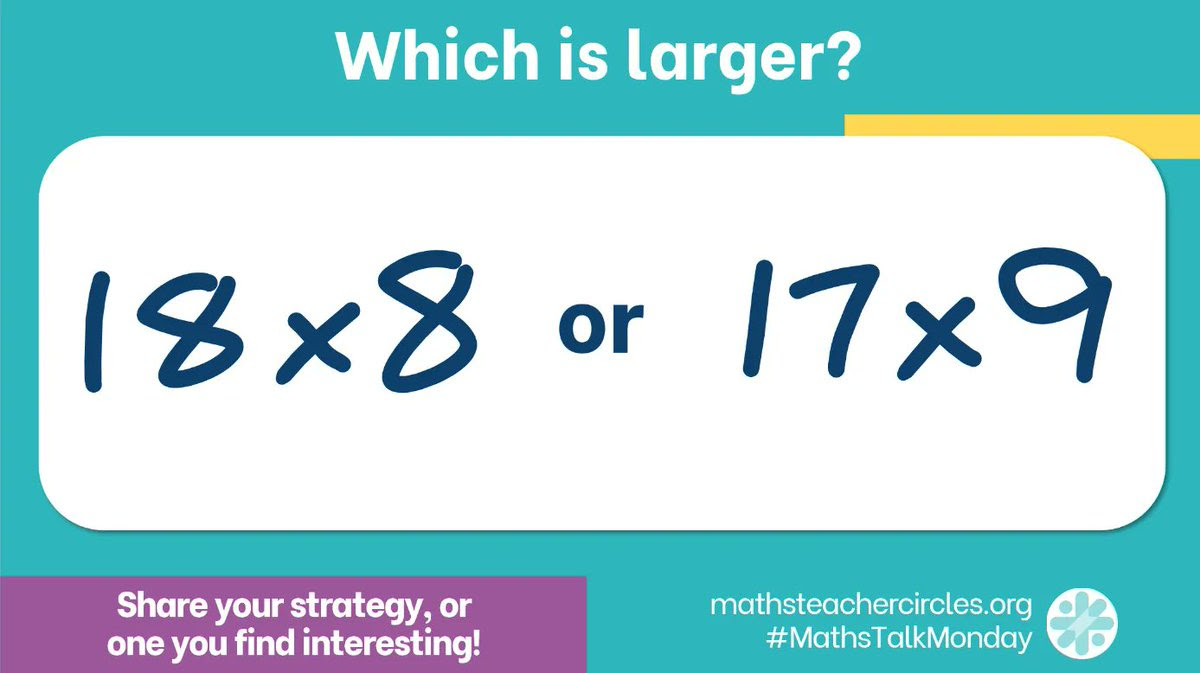
It's easy enough to just multiply them and see, but see if your students can figure out what method or reasoning each person used.
Which ones make sense to you?
Which one is the most clever?
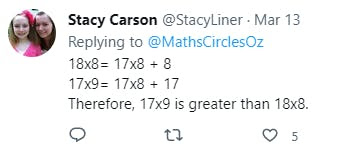
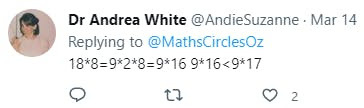
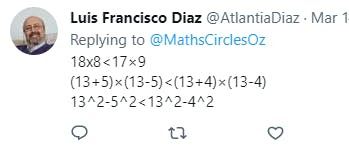
.: [], [internet], [New].
. . . View This Fullsize
Which is better?
I have explained like 1,000 times this year that "exact" answer means leave it in terms of roots and \( \pi \) etc, but kids interpret a crazy decimal as more "exact" lol.
Anyone have better verbiage?— Bowman Dickson 🏳️🌈 (@bowmanimal)
.: [], [internet], [New].
. . . View This Fullsize
TickTokMaths considers this the worst problem ever because the area and perimeter are the same numerical values, so students might find the area by adding up the sides.
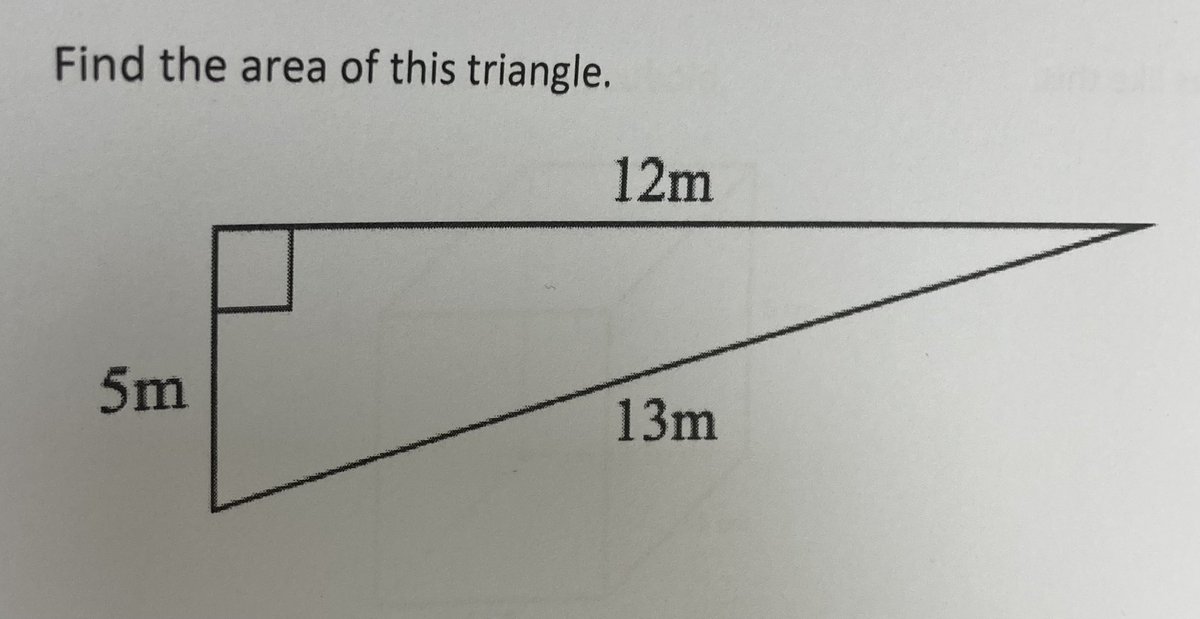
What are some other shapes that have the same numerical value of perimeter and area? (Understanding that perimeter is \( m \) and area is \( m^2 \) )
.: [], [internet], [New].
. . . View This Fullsize
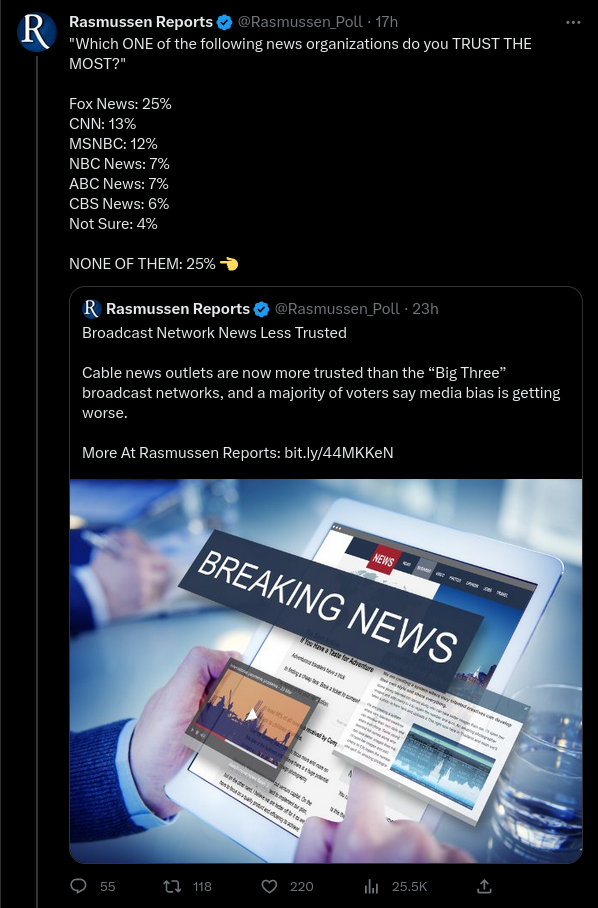
You could legitimately interpret this as
Right leaning: 25%What other ways could you interpret this set of results?
Left leaning: 45%
Print and Internet: 25%
.: [], [internet], [New].
. . . View This Fullsize
Instructions for Mimizu
1. Numbers are entered in order.
2. Light gray walls are "open". Adjacent hexagons with an opening must be consecutive OR share a common prime factor.
Conversely, consecutive hexagons or hexagons that share a
common factor must have an open wall between them.
3. Solid black walls are "Closed". Adjacent hexagons with a wall cannot be consecutive AND cannot share a common prime
number … and vice-versa.
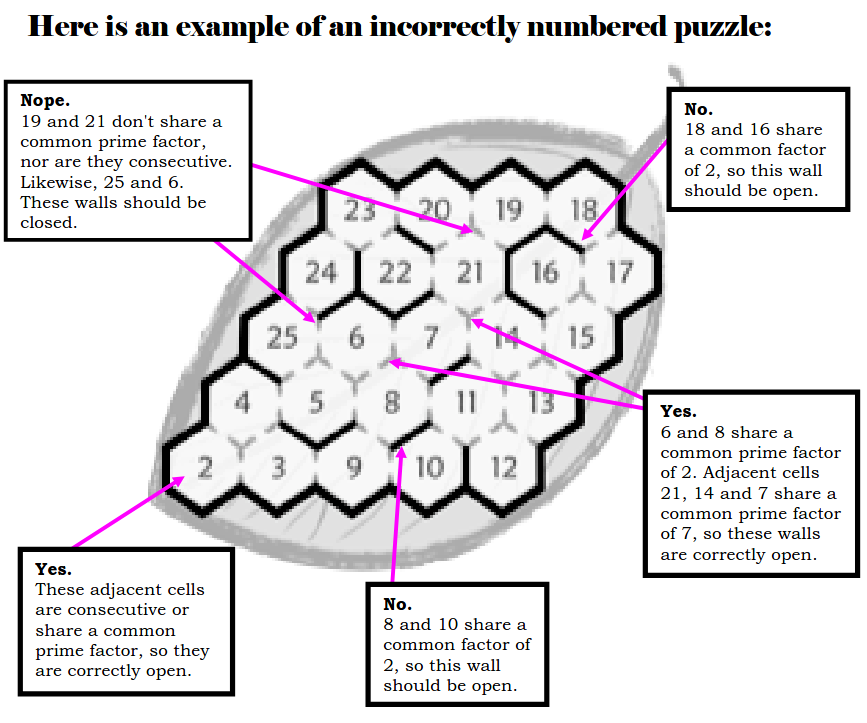
Here are a few puzzles.
.: [], [internet], [New].