Math Arguments
Problems, Questions, and Puzzles to spark discussion and argument in the maths classroom.
The Conical Tank
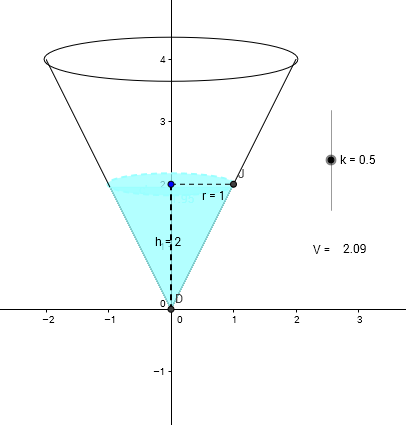
The last of the three related-rate geogebra problems from Kate Nowak. It's the related rate problem from calculus: the conical tank being filled with water.
Adjust the slider and... wait, what is changing and how?
For every click of the slider:
Is the depth increasing at a constant rate?
Is the radius increasing at a constant rate?
Is the volume increasing at a constant rate?
How can you tell?
- Where or how, in the RealWorldtm, could we see the constant increase in volume?
- Where or how, in the RealWorldtm, could we see the constant increase in radius, or depth?
.
More Information:
 ++
++