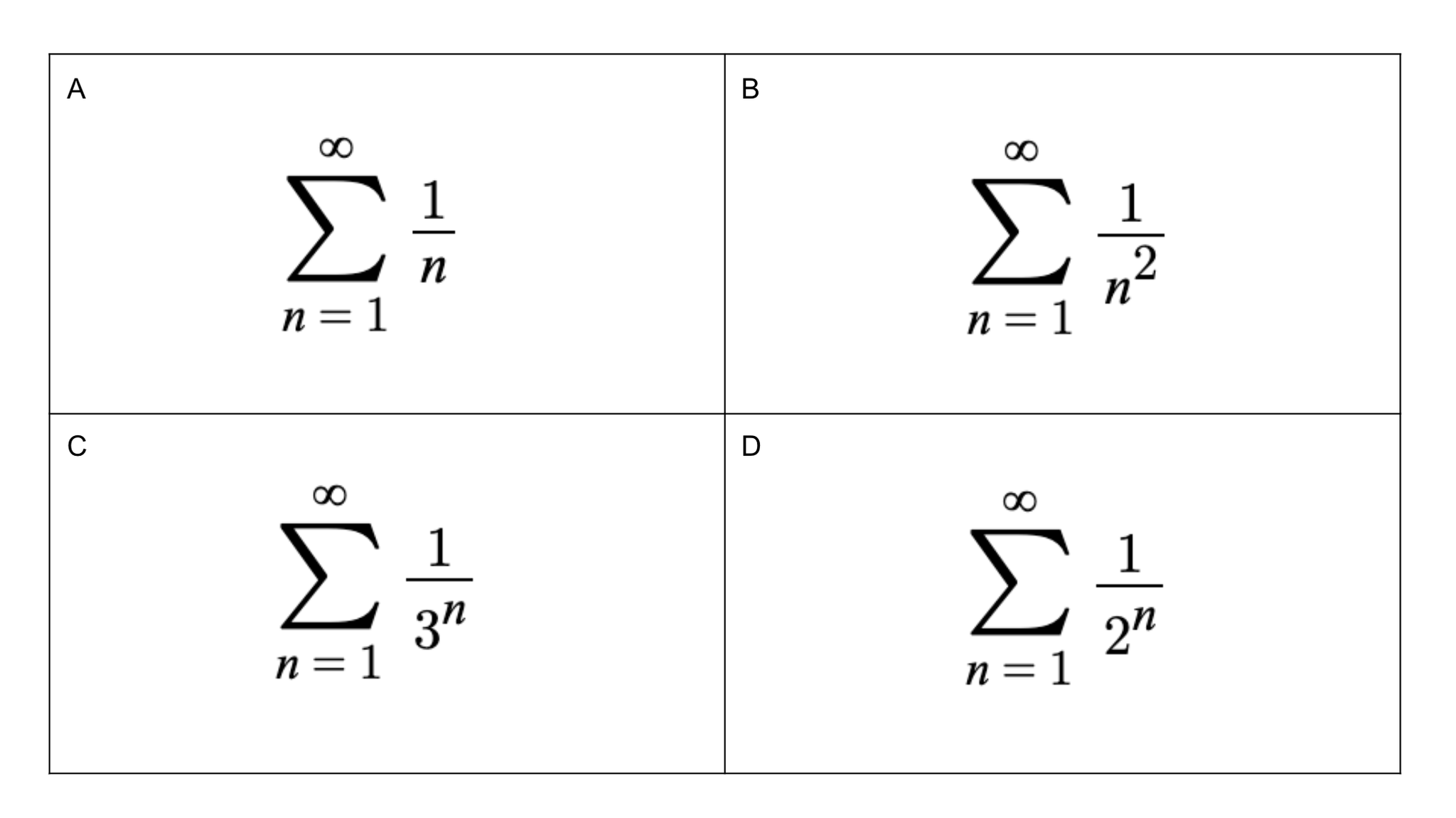12 of 12 Items .... Course: CALC

. . . View This Fullsize

Help me understand the fundamental definition of concavity.
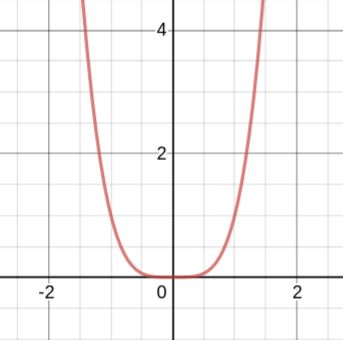
Consider the function \(y = x^4 \)

Can we say that is concave up from \((-\infty, +\infty)\)
or do we need to say \( (-\infty,0) \cup(0,+\infty) \)?

Here is it, if you want to see a visual.

. . . View This Fullsize

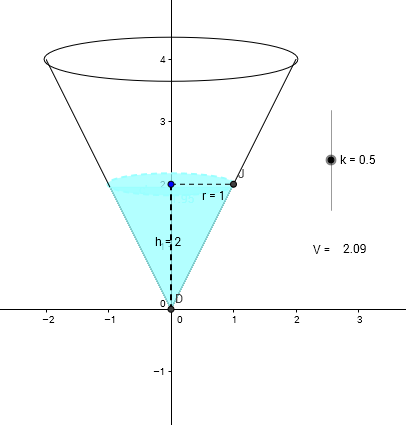
The last of the three related-rate geogebra problems from Kate Nowak. It's the related rate problem from calculus: the conical tank being filled with water.

Adjust the slider and... wait, what is changing and how?

For every click of the slider:
Is the depth increasing at a constant rate?
Is the radius increasing at a constant rate?
Is the volume increasing at a constant rate?
How can you tell?

• Where or how, in the RealWorld^tm, could we see the constant increase in volume?


• Where or how, in the RealWorld^tm, could we see the constant increase in radius, or depth?

. . . View This Fullsize

We've all seen this problem, but many of our students haven't. It's the related rate problem from calculus: the balloon being filled with air.

There are two questions being demonstrated here.
(1) "If the volume increases at a constant rate, what is happening to the radius?" and
(2) "If the radius increases at a constant rate, what is happening to the volume?"

The first question is to figure out which situation is modeled in red and which in blue.
Then we can ask:

• Does the radius increase at a constant speed in both models? How can you tell?


• Does the volume increase at a constant speed in both models? How can you tell?


• Where or how, in the RealWorld^tm, could we see the constant increase in volume?


• Where or how, in the RealWorld^tm, could we see the constant increase in radius?

. . . View This Fullsize

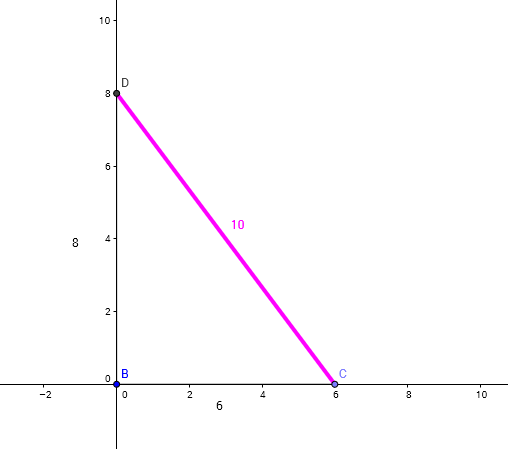
We've all seen this problem, but many of our students haven't.

It's the related rate problem from calculus: the ladder sliding down the wall.

The "official" question?

How fast is the ladder's top sliding down the wall if the bottom is being pulled out at a rate of 1 ft/sec?

We can ask a few questions of kids at any level, though, based on the given that the bottom of the ladder is being pulled to the right at 1 foot per sec.

• Does the top drop at a constant speed?


• Does the top drop a distance equal to the horizontal movement?


• When is the speed of the top greater than 1, less than 1, and equal to 1?


• If this is a 25 foot ladder, with the bottom 7 feet out from the base of the wall, and the top drops 4 feet ... how far out does the bottom of the ladder have to go?

. . . View This Fullsize

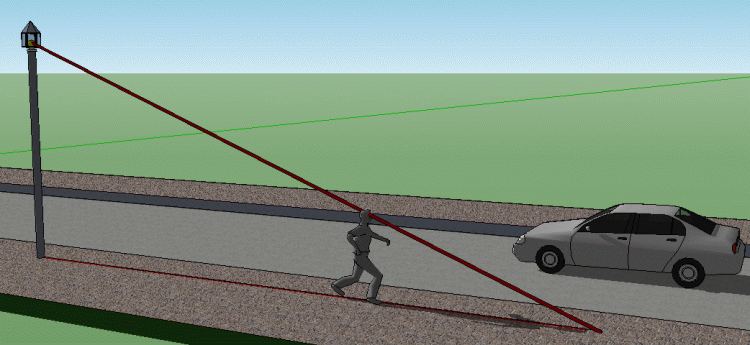
The man is walking down the sidewalk in the evening, at a constant speed. As he walks away from the streetlight, he casts a shadow in front of him.

If a second man were to try and keep up with the very front tip of his shadow, would he be walking at a constant speed, accelerating or decelerating, or what?

How do you know your answer is correct?

. . . View This Fullsize

Describe how the two trucks must work together throughout this turn.
Does either vehicle stop during the turn?
How would you coordinate this?

. . . View This Fullsize

Pascal's Triangle can be used to demonstrate how the Power Rule works in finding the derivative.

Wait, what?




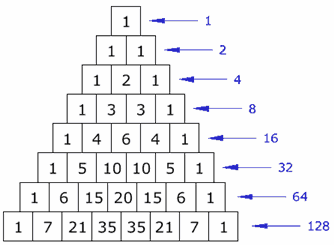
How does that help us with the limit definition of the derivative? Is there a shortcut?

\(f'(x) = \displaystyle\lim_{h\rightarrow 0} \dfrac{f(x+h)-f(x)}{h}\)

. . . View This Fullsize

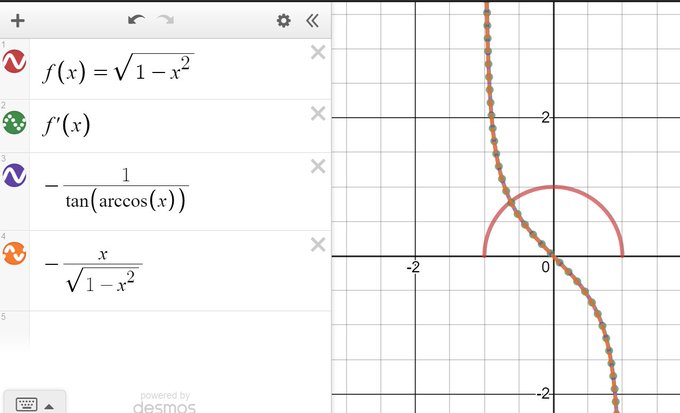
Set out to find the derivative of a semi-circle. I am intrigued but sort of confused. Are these the same thing?

. . . View This Fullsize

. . . View This Fullsize

. . . View This Fullsize

. . . View This Fullsize

Consider the following graph of \( y=\sqrt{x} \)
What is happening at (0,0)?




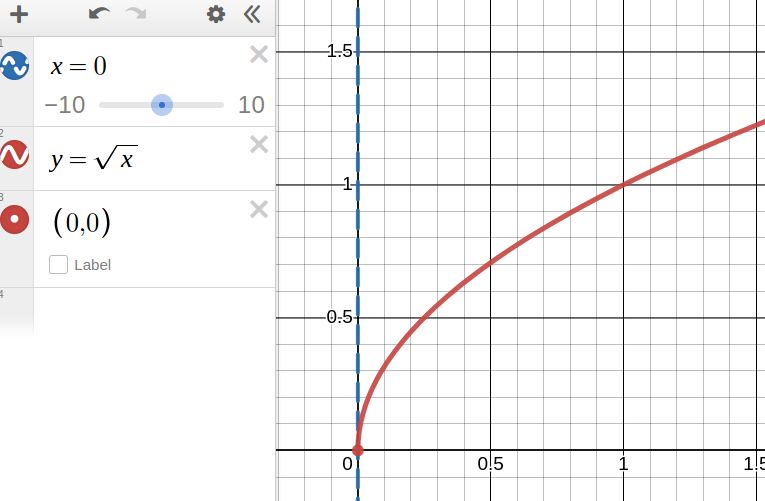
Is \( x=0 \) an asymptote?
Is this a jump discontinuity at \( x=0 \)?
Point discontinuity?
Asymptote discontinuity?
Infinite Discontinuity?
Tangent?

Do we need a new term?

What do you think?