12 of 34 Items .... Type: Understandings
Problems, Questions, and Puzzles to spark discussion and argument in the maths classroom.
Navigation:
- by Source
- by Course
.... - Problem Type: 101 Things
3ACT
ASN
ChatGPT
Combinatorics
Comparisons
Constructions
Create a Problem
DebateMath
Definitions
DESMOS Art
Desmos Challenge
DoThis
Epiphany
Equity
Explainer
Find the Error
Find the Pattern
Game
Geometry Snacks
Graphicacy
Graphical Approach
How Many Ways?
How Many?
Illusion
Impossible Problem
MathArt
MathStrategy
MathTip
Meme
Mimizu
Modeling
New
New Understanding
Notation
Notice, Wonder
Number Theory
Number_Search
Number_Talks
Open Middle
Optimization
Pedagogy
Policy
Proof Without Words
Puzzle
Rates
Ratios & Proportions
Raw Pure Math
Regressions
Sensible?
Sidewalk Chalk
Smart Substitution
Starters
Strategy
Terminology
The Hook
The RealWorld
Topology
Understandings
VennWords
Wait. Really?
WCYDWT
What If
What is This?
What Questions
Which Would You Choose?
WODB
Yohaku
. . . View This Fullsize
Can you come up with other, better, divisions?
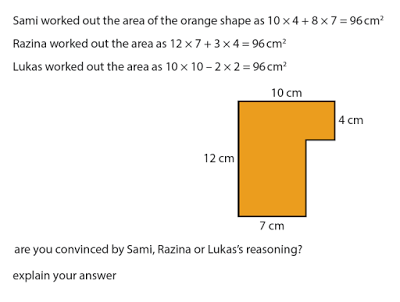
.: [GEOM], [Don Steward], [Understandings].
. . . View This Fullsize
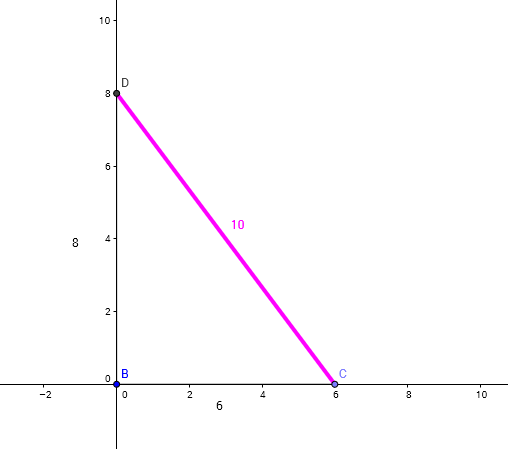
We've all seen this problem, but many of our students haven't.
It's the related rate problem from calculus: the ladder sliding down the wall.
The "official" question?
How fast is the ladder's top sliding down the wall if the bottom is being pulled out at a rate of 1 ft/sec?
We can ask a few questions of kids at any level, though, based on the given that the bottom of the ladder is being pulled to the right at 1 foot per sec.
- Does the top drop at a constant speed?
- Does the top drop a distance equal to the horizontal movement?
- When is the speed of the top greater than 1, less than 1, and equal to 1?
- If this is a 25 foot ladder, with the bottom 7 feet out from the base of the wall, and the top drops 4 feet ... how far out does the bottom of the ladder have to go?
.: [CALC], [Kate Nowak], [Understandings].
. . . View This Fullsize
If the proportion of blonds among blue-eyed people is greater than among the population as a whole, is it also true that the proportion of blue-eyed people among blonds is greater than among the population as a whole?
.: [ALL], [Futility Closet], [Understandings].
. . . View This Fullsize
You've all seen Plinko and its variations. Here's one:

This one has a normal curve drawn on the background. Should it be a normal curve or more triangular like the arrangement of the pins?
Would it still be in this shape if the pins were arranged in a rectangle?
.: [STATS], [Curmudgeon], [Understandings].
. . . View This Fullsize
The floor lamp casts a shadow.
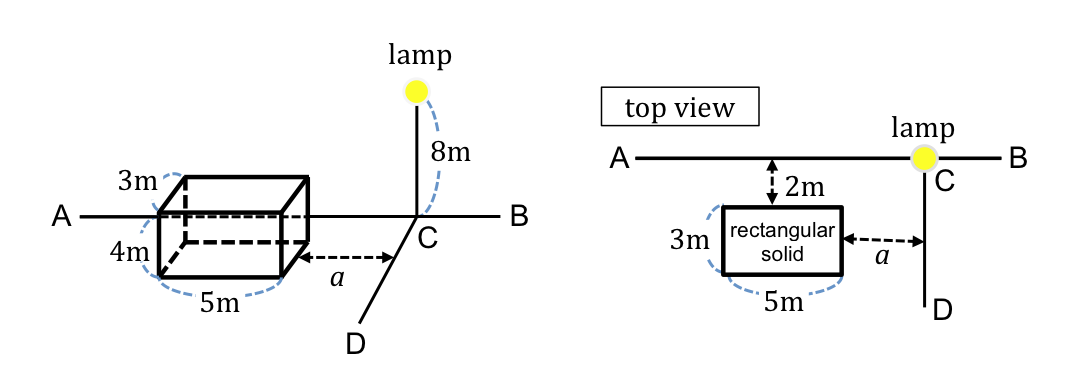
Straight line AB is drawn on a wide, spacious floor. A lamp is at a height of 8m above point C, which is located on line AB. Line CD is perpendicular to line AB. A rectangular solid 5m by 3m by 4m is on the floor as shown. The box is 2m from line AB and a meters from line CD. Assume the lamp is a point source and will cast a perfect shadow. Given that the rectangular solid casts a shadow with area \(90m^2\), determine the distance a (in meters).
- Does the 2m distance from the wall matter to the shape of the shadow?
- How does the distance a change the area of the shadow?
- What shape is that shadow on the floor?
- Are the edges of the shadow guaranteed to parallel with the edges of the box?
- How far away is that box from the light?
.: [PHYSICS], [Five Triangles], [Understandings].
. . . View This Fullsize
\( x^2 = 81 \) has two solutions, -9 and 9.
But does \( \sqrt{81} \) have one solution or two?
Is it correct to say that \( \sqrt{81} \) = +9 and -9?
Or should we be saying that \( \sqrt{81} \) is an expression and that \( 9\), \(\frac{18}{2} \), \(27^{2/3} \), and \(1+6+2\), are equivalent expressions?
.: [ALG1], [Kate Nowak], [Understandings].
. . . View This Fullsize
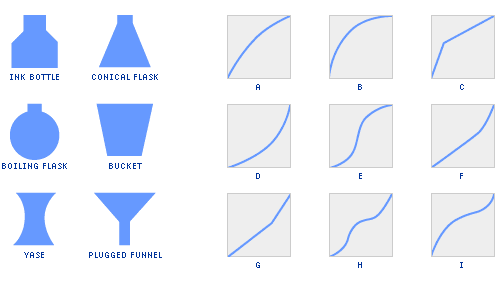
Imagine you were filling each bottle with water, poured at a constant rate.
Which bottle fits which height-time graph.
Draw the bottles for the remaining graphs.
.: [GEOM], [internet], [Understandings].
. . . View This Fullsize

Suppose that a white Rubik's Cube is painted blue on top and bottom and painted red on the four lateral sides. The cube is then separated into its 27 smaller cubes.
How many unit cubes have at least one red face and one blue face?
.: [LOGIC], [Curmudgeon], [Understandings].
. . . View This Fullsize
As we all know, the questions in an SAT test get harder as you get to the end of a section. I warn my students repeatedly that, as they approach the end of a section,
"If you can't see what all those people thought was the obvious answer ...You see, the question at the end aren't really difficult usually. They can be badly worded but they're rarely HARD. They are usually four-step problems that everyone else is so sure about, and the answer is so obvious that they get suckered in. These two were rated the same level of difficulty, and were answered correctly by about 3%-5% of the students.
and clearly see why that obvious answer is wrong, ...
then you are one of those who will jump to the wrong conclusion and you'll get it wrong, too."
Which one is harder?
25. A woman drives to work each day at an average speed of 40 miles per hour and returns along the same route at 30 miles per hour. If her total traveling time was 1 hour, what was the total number of miles in the trip?
- 30
- \(30\dfrac{1}{7}\)
- \(34\dfrac{2}{7}\)
- 35
- 40
24. A 25 foot ladder is placed against a vertical wall of a building with the bottom of the ladder standing on concrete 7 feet from the base of the building. If the top of the ladder slips down 4 feet, then the bottom of the ladder will slide out.
- 4ft
- 5ft
- 6ft
- 7ft
- 8ft
In each case, can you say why the obvious answer is wrong?
.: [SAT], [T.R.Milne], [Understandings].
. . . View This Fullsize
Can a line be tangent to a circle? Sure, if they're coplanar.
What if they're NOT co-planar?
.: [GEOM], [internet], [Understandings].
. . . View This Fullsize
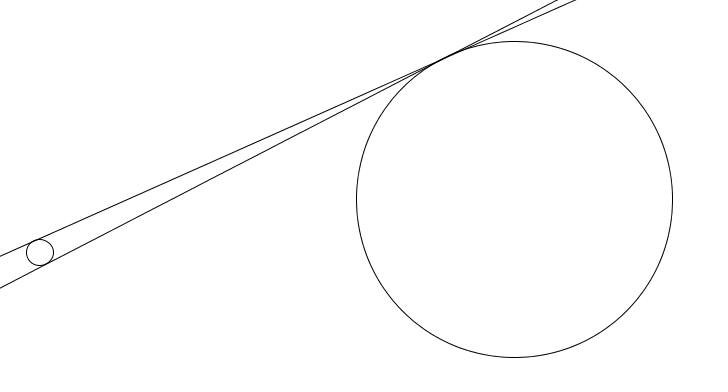
Given: 2 common tangent lines, one external and one internal.
The question was raised as to whether the large circle could be tangent to both lines at the intersection point. What do you think?
The fun part, of course, is "Can you explain that to the English teacher?" (force them to be clear but not too technical). If those are tangents, can the circle go through the intersection point, even if not tangentially?
.: [GEOM], [internet], [Understandings].
. . . View This Fullsize
Can two lines of infinite length be considered congruent?
.: [GEOM], [Justin Aion], [Understandings].