12 of 13 Items .... Type: Strategy
Problems, Questions, and Puzzles to spark discussion and argument in the maths classroom.
Navigation:
- by Source
- by Course
.... - Problem Type: 101 Things
3ACT
ASN
ChatGPT
Combinatorics
Comparisons
Constructions
Create a Problem
DebateMath
Definitions
DESMOS Art
Desmos Challenge
DoThis
Epiphany
Equity
Explainer
Find the Error
Find the Pattern
Game
Geometry Snacks
Graphicacy
Graphical Approach
How Many Ways?
How Many?
Illusion
Impossible Problem
MathArt
MathStrategy
MathTip
Meme
Mimizu
Modeling
New
New Understanding
Notation
Notice, Wonder
Number Theory
Number_Search
Number_Talks
Open Middle
Optimization
Pedagogy
Policy
Proof Without Words
Puzzle
Rates
Ratios & Proportions
Raw Pure Math
Regressions
Sensible?
Sidewalk Chalk
Smart Substitution
Starters
Strategy
Terminology
The Hook
The RealWorld
Topology
Understandings
VennWords
Wait. Really?
WCYDWT
What If
What is This?
What Questions
Which Would You Choose?
WODB
Yohaku
. . . View This Fullsize
That's pretty much it: How many Geometry Theorems are needed to solve this extended problem?
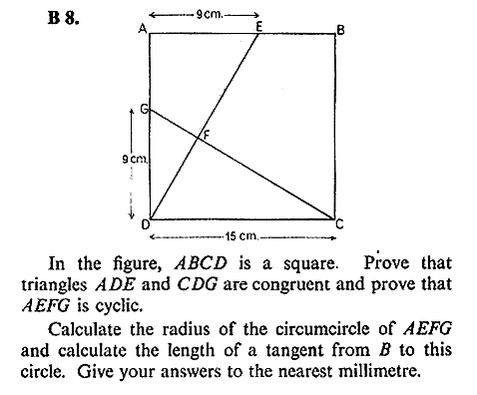
.: [GEOM], [SolveMyMaths], [Strategy].
. . . View This Fullsize
Skimming the MTBoS Finds Interesting Things video from the Global Math department.
Which will be more likely to occur first
in a string of coin tosses, HTH or HTT?
This is the kind of question that becomes difficult because of assumptions made by the listener, assumptions that change the problem subtly and thus change the resulting expected probability.
The listener/reader here naturally changes this question to "Which group of three is more likely?", but that is not what he asked. We should refer back to the Monty Hall question.
.: [PROBABILTY], [Bob Lochel], [Strategy].
. . . View This Fullsize

Equilateral triangles tile the plane. Is it possible to select four intersection points that are the corners of a perfect square?
.: [GEOM], [James Tanton], [Strategy].
. . . View This Fullsize
Could this work? What might go wrong with this plan?

If you divided the pizza into EIGHT pieces, what would be your chances of having to pay?
.: [PROBABILTY], [T.R.Milne], [Strategy].
. . . View This Fullsize
What is the best way to find the perimeter of the rounded hexagonal shape, i.e., the length of the belt that would wrap around the six wheels?
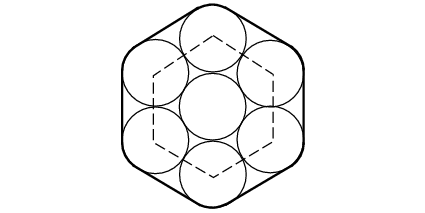
Radius of each pulley is \(1\)
.: [GEOM], [T.R.Milne], [Strategy].
. . . View This Fullsize
Assuming that you get every question correct, and bet it all on the Daily Double, and the Daily Double happens at the most opportune time, and the Daily double is located in the absolute best place, how much can you win in the first round of Jeopardy?
And what is the best place for the Daily Double?
And the best time to get the Daily Double?

The prizes are twice as big when you get to the Double Jeopardy Round:

So let's keep this going ... how much can you theoretically win to this point?
In Final Jeopardy, you can bet it all ("Let it Ride", as gamblers say).

.: [LOGIC], [T.R.Milne], [Strategy].
. . . View This Fullsize
For what value(s) of \(x\) is \(x^2+x+1=2x\sqrt{x+1}\)?
There are many ways to solve this. Wolframalpha, DESMOS. or Geogebra will all give an answer but can you decipher the clues in the heading?
Look at the graphs for the equation in Wolfram. The curves appear to be tangent to each other at the point of intersection. Can you show this to be true? or not?
.: [PRE-CALC], [David Marain], [Strategy].
. . . View This Fullsize
\( tan(23^{\circ}) = \dfrac{274}{x} \)
What do you know about the size of \( x \)? Is it longer or shorter than 274?
What if the angle were \( -23^{\circ} \)?
What other values of \( x \) are possible?
Sketch the triangle and find the value of \( x \).
.: [GEOM], [T.R.Milne], [Strategy].
. . . View This Fullsize
\( sin(\theta) = \dfrac{274}{391} \)
What if the fraction were \( -\dfrac{274}{391} \)?
What do you know about the size of \( \theta \), compared to the common angles?
What other values of \( \theta \) are possible?
Sketch the triangle and find the value of \( \theta \).
.: [GEOM], [T.R.Milne], [Strategy].
. . . View This Fullsize
You are 1 of 999,999 people asked. You get to keep whatever 6-digit dollar amount you want as long as no one else chooses it. What do you choose?
.: [PROBABILTY], [T.R.Milne], [Strategy].
. . . View This Fullsize
What method would you use to answer this question?
Are there any other methods can you think of?
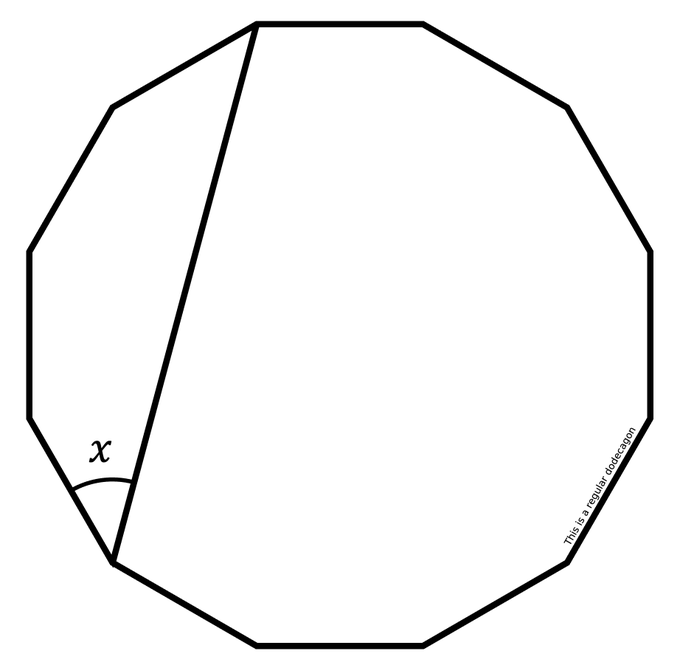
Can you generalise your method?
Suppose x = f(n,s) where for this question, n = 12, and s = 3.
Can you find a general form for f(n,3)?
How about f(12,s)?
How about f(n,s)?
.: [GEOM], [Nathan Day], [Strategy].
