12 of 32 Items .... Type: Raw Pure Math
Problems, Questions, and Puzzles to spark discussion and argument in the maths classroom.
Navigation:
- by Source
- by Course
.... - Problem Type: 101 Things
3ACT
ASN
ChatGPT
Combinatorics
Comparisons
Constructions
Create a Problem
DebateMath
Definitions
DESMOS Art
Desmos Challenge
DoThis
Epiphany
Equity
Explainer
Find the Error
Find the Pattern
Game
Geometry Snacks
Graphicacy
Graphical Approach
How Many Ways?
How Many?
Illusion
Impossible Problem
MathArt
MathStrategy
MathTip
Meme
Mimizu
Modeling
New
New Understanding
Notation
Notice, Wonder
Number Theory
Number_Search
Number_Talks
Open Middle
Optimization
Pedagogy
Policy
Proof Without Words
Puzzle
Rates
Ratios & Proportions
Raw Pure Math
Regressions
Sensible?
Sidewalk Chalk
Smart Substitution
Starters
Strategy
Terminology
The Hook
The RealWorld
Topology
Understandings
VennWords
Wait. Really?
WCYDWT
What If
What is This?
What Questions
Which Would You Choose?
WODB
Yohaku
. . . View This Fullsize
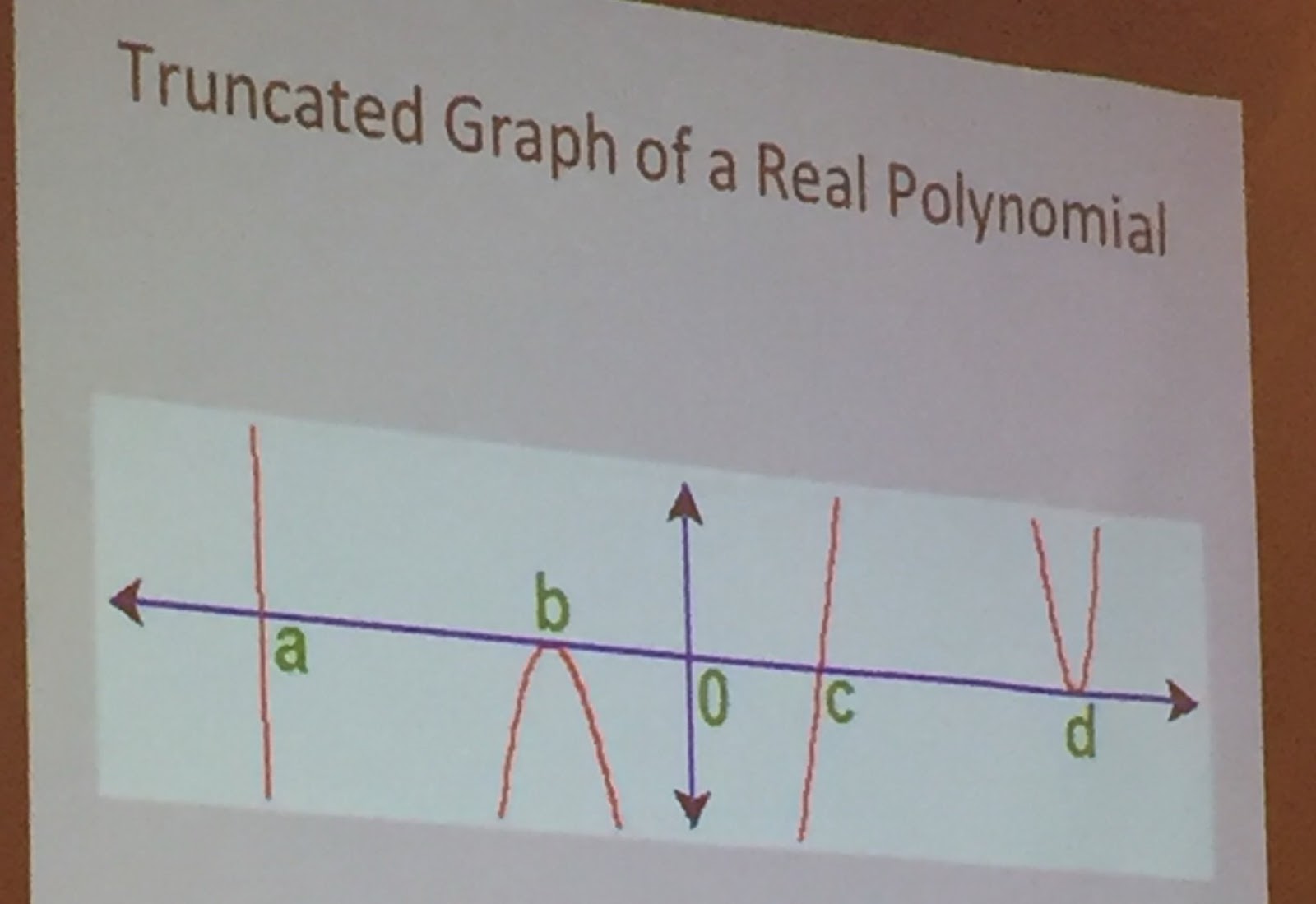
Algebra 2:
Write a function for this graph ...
Estimation:
What are some possible values for a,b,c,d?
If I told you it also went through (0,54), what might the leading coefficient be?
.: [ALG2], [Jennifer Wilson], [Raw Pure Math].
. . . View This Fullsize
If we stipulate that
\( (x+12)^2+(y+4)^2+(z+3)^2=0\), then
\( \sqrt{x^2+y^2+z^2}=?\)
Should we brute-force this or is there a more beautiful or subtle way of getting what we want?
.: [PRE-CALC], [David Marain], [Raw Pure Math].
. . . View This Fullsize
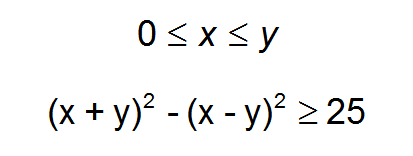
Is there enough information to determine the least possible value of y?
.: [PRE-CALC], [SAT], [Raw Pure Math].
. . . View This Fullsize
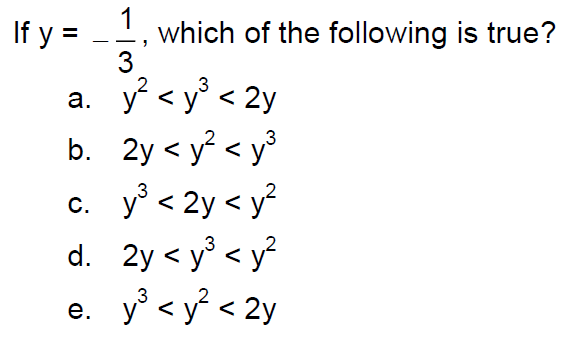
Can you find values for y that will make each answer true? Generalize the rules in effect here.
.: [ALG2], [SAT], [Raw Pure Math].
. . . View This Fullsize
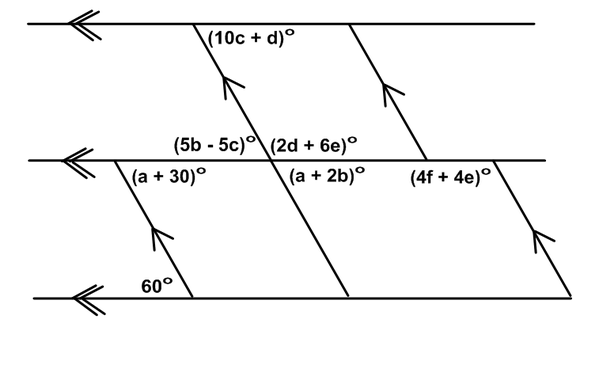
Raw, pure math. Ummmmmm, tasty.
But can you make the question harder by rearranging the variables?
.: [GEOM], [mathsjem], [Raw Pure Math].
. . . View This Fullsize
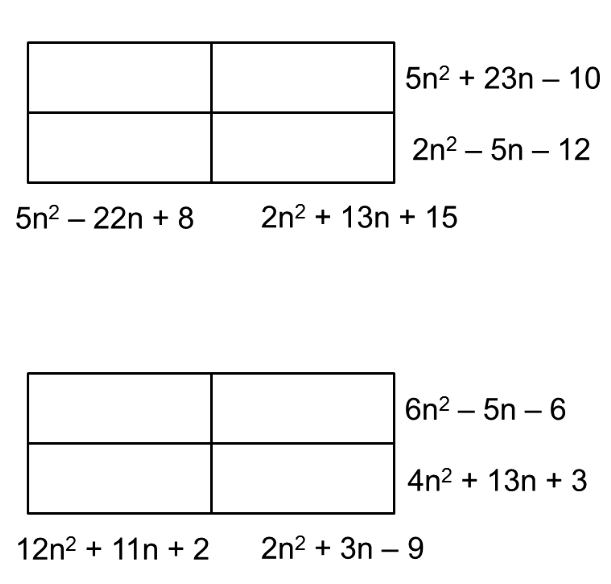
For the last couple of days, I've been asking you to create a new puzzle. Today, I'd like you to describe HOW to create a puzzle with a unique solution, or two solutions, or three. How did Don Steward create these and KNOW that they only had one solution?
.: [ALG2], [Don Steward], [Raw Pure Math].
. . . View This Fullsize
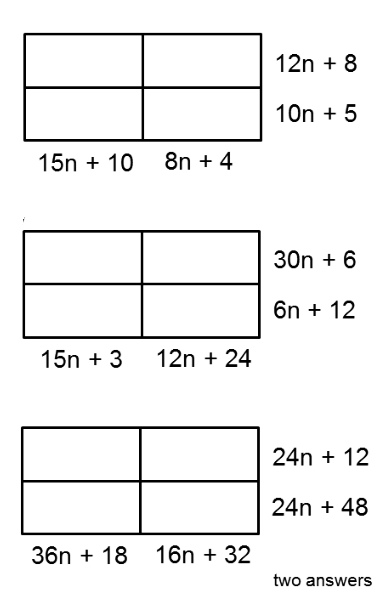
Put algebraic expressions into the cells so that the product is as indicated. That's for warm-up.
That's not what I'm going to ask you to do, though ...
Make a new puzzle with two solutions.
.: [ALG2], [Don Steward], [Raw Pure Math].
. . . View This Fullsize
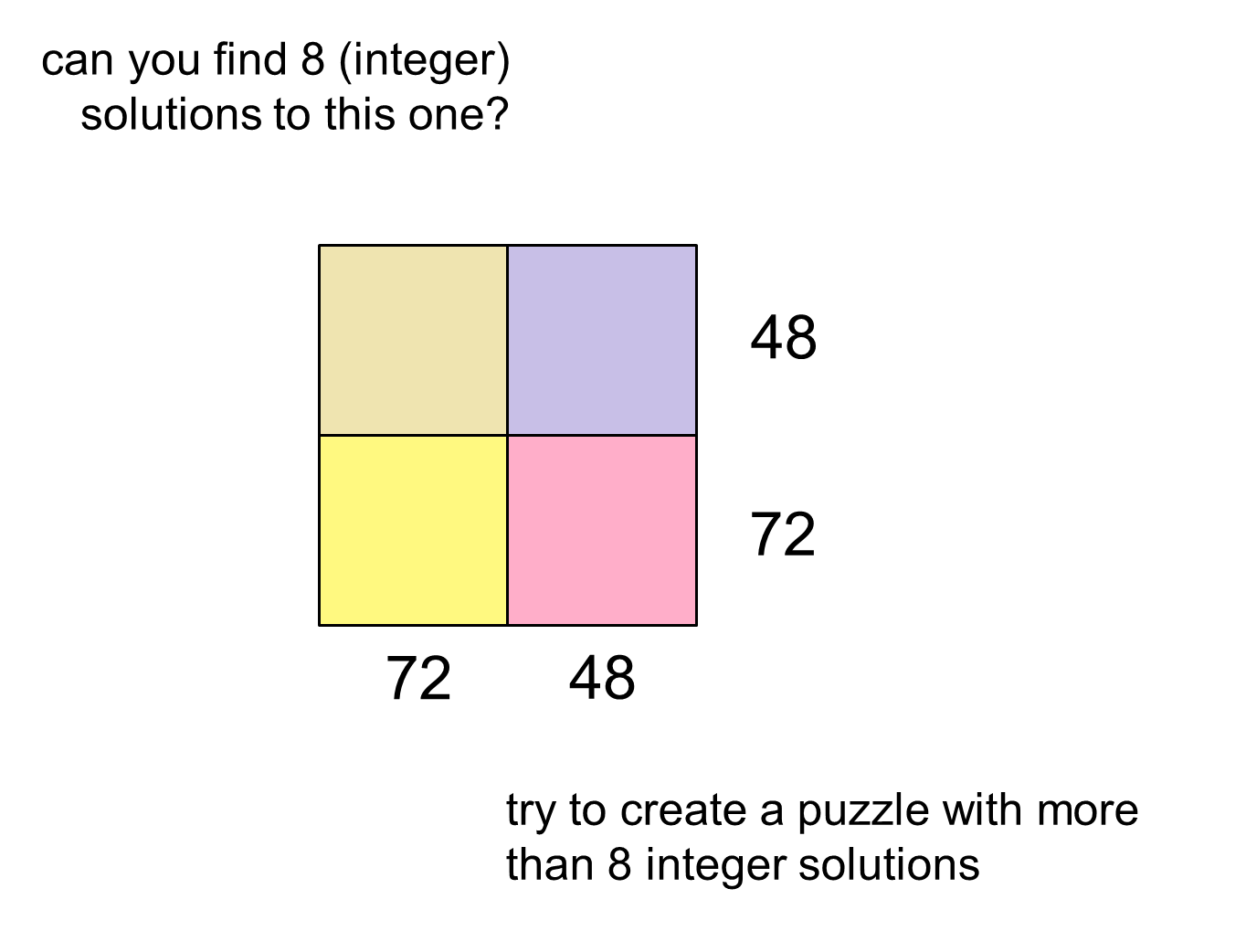
Put integers into the cells so that their product is as indicated.
.: [MS Math], [Don Steward], [Raw Pure Math].
. . . View This Fullsize
list all possible ordered pairs (a,b).
What are a couple of different ways to approach this nugget?
What are the "obvious" answers that everyone will miss?
.: [ALG2], [David Marain], [Raw Pure Math].
. . . View This Fullsize
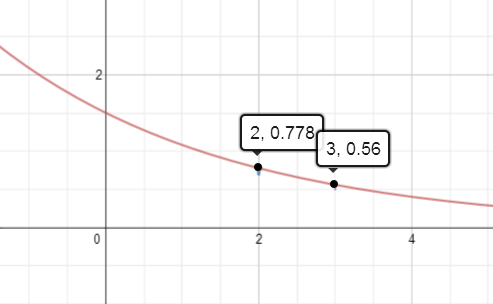
Is this enough information to find the equation?
.: [ALG2], [T.R.Milne], [Raw Pure Math].
. . . View This Fullsize
Let's examine the function g(n):
g(n) = smallest integer such that g(n)*n! is a perfect square.
How should we go about finding if there's a pattern in that?
.: [PRE-CALC], [James Tanton], [Raw Pure Math].
. . . View This Fullsize
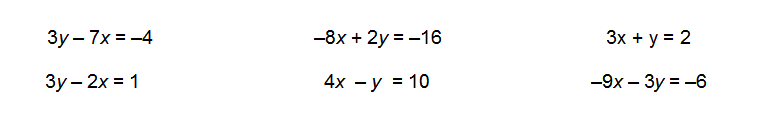
Is there an easy way to tell if those lines will have one solution, no solution, or an infinite number of solutions?
.: [ALG1], [T.R.Milne], [Raw Pure Math].