12 of 80 Items .... Type: Number Theory

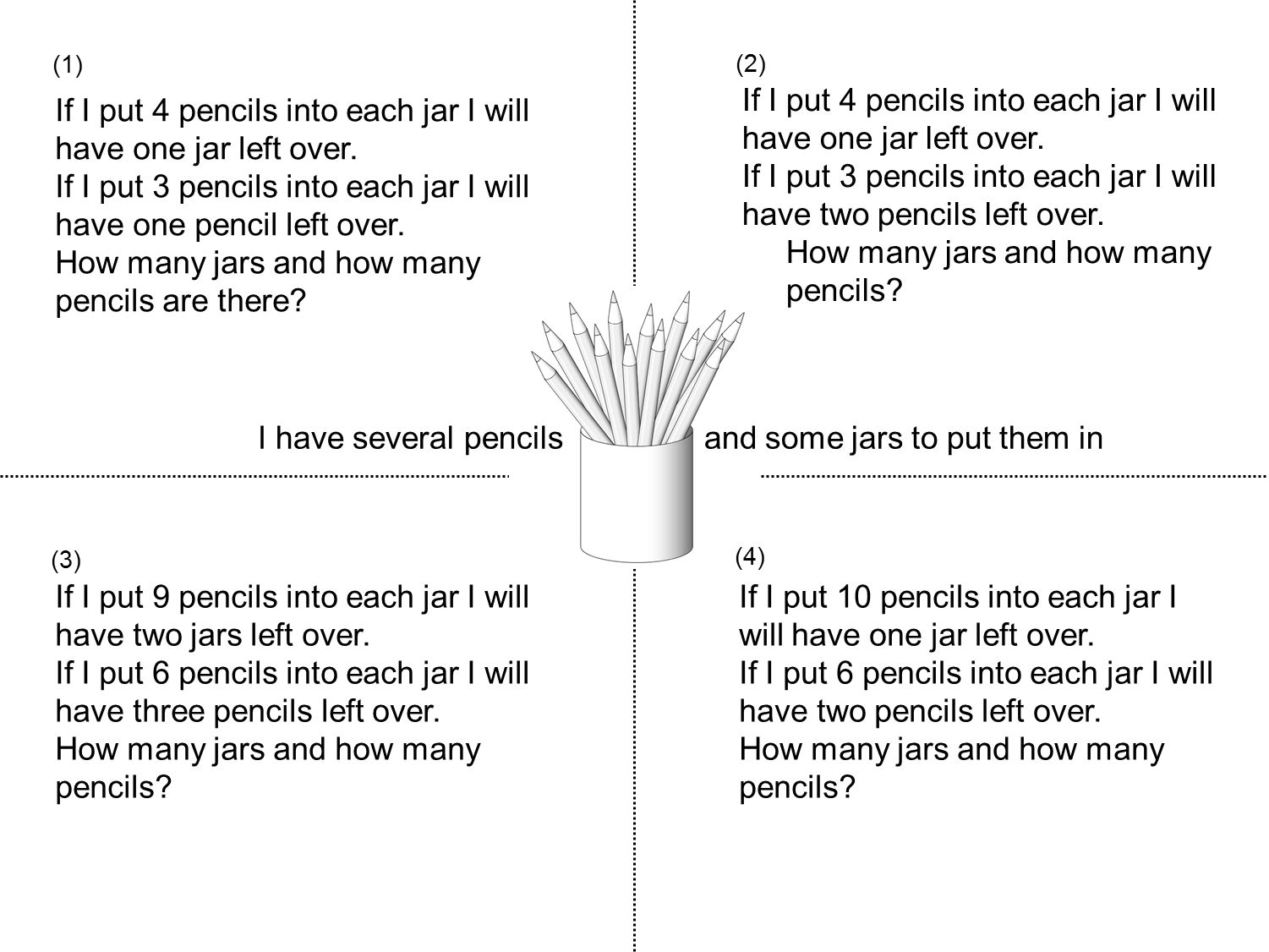
An interesting Question ... is an algebraic method the only way to do this?

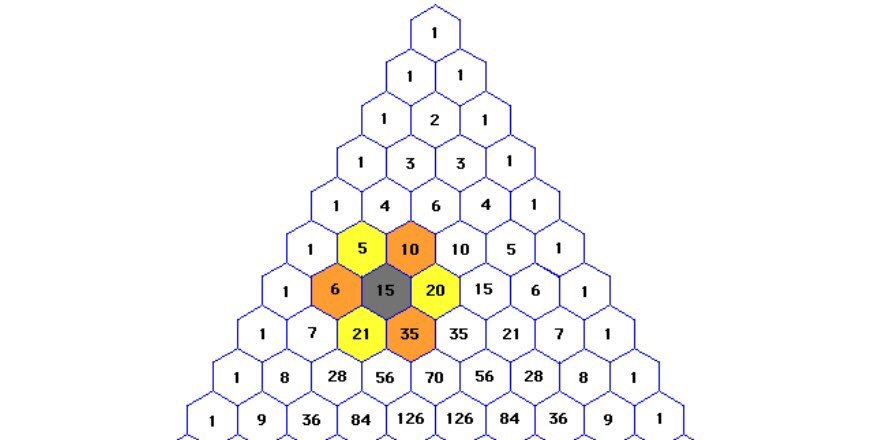
Prove that anywhere on Pascal's triangle, products of numbers in yellow and in orange are equal.

.: [ALG1], [Five Triangles], [Number Theory].

. . . View This Fullsize

A quick probability question ...

Player A's score is determined by taking the highest of 3 dice.
Player B's is determined by taking second-highest of 8.
Who wins more games?

.: [PROBABILTY], [Ben Orlin], [Number Theory].

. . . View This Fullsize

Marilyn Burns pointed out:

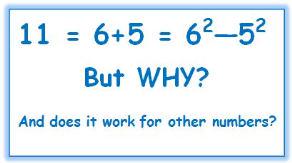
Well, does it?
Is there a pattern that always works?

.: [ALG1], [internet], [Number Theory].

. . . View This Fullsize

On a number line, how many positive integers are closer to 50 than to 100?

.: [ALL], [David Marain], [Number Theory].

. . . View This Fullsize

What insights does a student need to have before this problem is solvable?

.: [Teacher Education], [T.R.Milne], [Number Theory].

. . . View This Fullsize

We all recognize the Fibonacci Sequence: 1, 1, 2, 3, 5, 8, 13, 21, ...
What is the units digit of the sixty-first Fibonacci number?

Is there a pattern?

.: [ALL], [James Tanton], [Number Theory].

. . . View This Fullsize

For how many integers k is \(10,000 - k^2\) positive?

.: [ALL], [David Marain], [Number Theory].

. . . View This Fullsize

Which mental path do you think is easiest for beginning students? (Analytical, numerical, graphical, algebraic?) Would you give a different hint to beginning students than to advanced students?

Will the average of \( 2^{48} \) & \( 2^{50}\) be less than, greater than, or equal to \( 2^{49} \)?

Can you find the actual average? (without a calculator!)

.: [SAT], [David Marain], [Number Theory].

. . . View This Fullsize

.: [MS Math], [Don Steward], [Number Theory].

. . . View This Fullsize

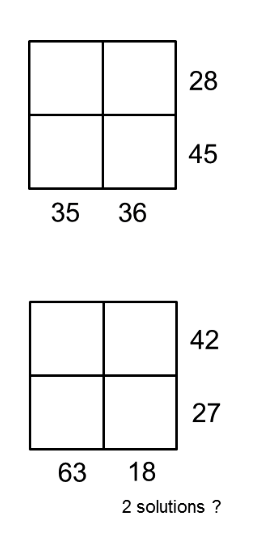
Put integers into the cells so that their product is as indicated. But that's not what I'm going to ask you to do, though ...

Make a puzzle with exactly 3 solutions.

.: [MS Math], [Don Steward], [Number Theory].

. . . View This Fullsize

How can we approach this beast of a problem without finding LCM?

\(\dfrac{1}{1} - \dfrac{5}{6} + \dfrac{7}{12} - \dfrac{9}{20} + \dfrac{11}{30} - \dfrac{13}{42} + \dfrac{15}{56} - \dfrac{17}{72} + \dfrac{19}{90} = \dfrac{a}{b}\)

.: [PREALG], [T.R.Milne], [Number Theory].

. . . View This Fullsize

This little puzzle, via @mathmovesu, asks for three consecutive prime numbers.

Is the guess and check method the best way to go here?

Which prime numbers are candidates and which ones can we safely ignore?

.: [ALL], [internet], [Number Theory].