12 of 22 Items .... Type: New Understanding
Problems, Questions, and Puzzles to spark discussion and argument in the maths classroom.
Navigation:
- by Source
- by Course
.... - Problem Type: 101 Things
3ACT
ASN
ChatGPT
Combinatorics
Comparisons
Constructions
Create a Problem
DebateMath
Definitions
DESMOS Art
Desmos Challenge
DoThis
Epiphany
Equity
Explainer
Find the Error
Find the Pattern
Game
Geometry Snacks
Graphicacy
Graphical Approach
How Many Ways?
How Many?
Illusion
Impossible Problem
MathArt
MathStrategy
MathTip
Meme
Mimizu
Modeling
New
New Understanding
Notation
Notice, Wonder
Number Theory
Number_Search
Number_Talks
Open Middle
Optimization
Pedagogy
Policy
Proof Without Words
Puzzle
Rates
Ratios & Proportions
Raw Pure Math
Regressions
Sensible?
Sidewalk Chalk
Smart Substitution
Starters
Strategy
Terminology
The Hook
The RealWorld
Topology
Understandings
VennWords
Wait. Really?
WCYDWT
What If
What is This?
What Questions
Which Would You Choose?
WODB
Yohaku
. . . View This Fullsize
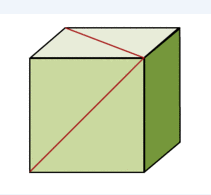
What's the angle between the red lines?
.: [GEOM], [internet], [New Understanding].
. . . View This Fullsize
To increase the volume of a cylinder, is it better to increase the radius or the height? Great conversation starter today.

.: [ALG1], [Patrick Honner], [New Understanding].
. . . View This Fullsize
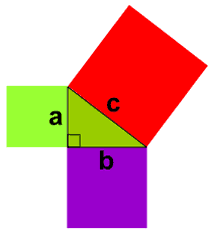
Pythagorean theorem: \(a^2 +b^2 = c^2\)
In a right triangle, the area of the square drawn on the hypotenuse is equal to the sum of the areas of the squares drawn on the other two legs.
Here is the problem: does the figure whose areas we compare, drawn on the triangle's legs, have to be square?
Can there be other shapes triangles, rhombuses, regular pentagons, etc. that make the Pythagorean Theorem more generally true?
.: [ALL], [Grant Wiggins], [New Understanding].
. . . View This Fullsize
I had asked "Is this really ok for a fifth-grader?
Five Triangles said, "We posed the question slightly differently, our diagram providing an important hint to bring it to a more manageable level for younger problem solvers."
Find \(x+y+z\)
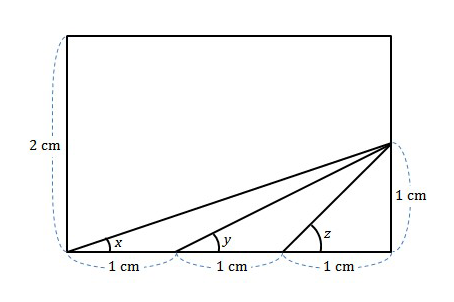
What do you suppose the "important hint" was?
.: [MS Math], [Five Triangles], [New Understanding].
. . . View This Fullsize
When the integers from 1 to 30 are multiplied, determine how many consecutive digits starting from the ones (1s) position are zeros.
Why does this question not require a calculator?
Would this be a fair question for some standardized test?
.: [ALL], [Five Triangles], [New Understanding].
. . . View This Fullsize
If we kept going, would any of the sides in this figure be parallel?

3
UPDATE: Asking a bad question is my fault. Of course, any polygon that has an even number of sides has n/2 pairs of parallel sides. What I was originally after, but didn't ask properly, was whether there will be a side of one polygon that is parallel to a side in another ... other than the pair in the triangle and square.
.: [GEOM], [T.R.Milne], [New Understanding].
. . . View This Fullsize
What is the largest even integer that cannot be written as the sum of two odd composite numbers?

R1
For example, 42 = 21 + 21, so it is not a candidate. 22 is a candidate because no pair of 9, 15, or 21 can equal 22.
As with many of Mr. Tanton's puzzles, there's a way to know that you are absolutely correct. Can you find the number and the explanation?
.: [ALL], [James Tanton], [New Understanding].
. . . View This Fullsize
I lied. It's not a Pythagorean triangle. It's TWO Pythagorean triangles that make up a Heronian triangle.
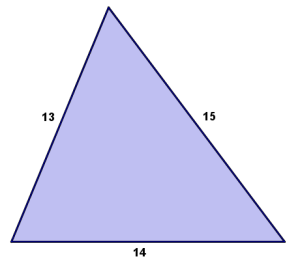
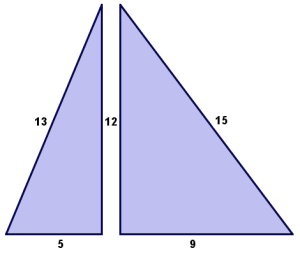
What other Pythagorean Triangle combinations make a triangle like this?
.: [MS Math], [internet], [New Understanding].
. . . View This Fullsize
All students with exactly 1 sibling, please stand.
If your sibling is of opposite sex, stay standing. Otherwise, sit down.
Do you predict half of them will stay standing? More than half? Less than half?
.: [PROBABILTY], [internet], [New Understanding].
. . . View This Fullsize
In the comments on 'More Exponents', Liz, on January 29th, said:
Wow, answer on Wolframalpha was pretty surprising! Is it true for all numbers \(a\) and \(b\), when \(a < b\), then \(a^b > b^a\)?
Well? What do you say, Internet?
.: [ALL], [internet], [New Understanding].
. . . View This Fullsize
Following on an earlier question from Day 7 ...
If I were to tell you that \(2^{100} - 100^2 = 1,267,650,600,228,229,401,496,703,195,376\),
can you tell me what would change if I hadn't subtracted \(100^2\)?
What is \(2^{100}\)?
How do you know?
Just for the record, what -illion is that?
.: [ALL], [T.R.Milne], [New Understanding].