12 of 19 Items .... Type: How Many Ways?
Problems, Questions, and Puzzles to spark discussion and argument in the maths classroom.
Navigation:
- by Source
- by Course
.... - Problem Type: 101 Things
3ACT
ASN
ChatGPT
Combinatorics
Comparisons
Constructions
Create a Problem
DebateMath
Definitions
DESMOS Art
Desmos Challenge
DoThis
Epiphany
Equity
Explainer
Find the Error
Find the Pattern
Game
Geometry Snacks
Graphicacy
Graphical Approach
How Many Ways?
How Many?
Illusion
Impossible Problem
MathArt
MathStrategy
MathTip
Meme
Mimizu
Modeling
New
New Understanding
Notation
Notice, Wonder
Number Theory
Number_Search
Number_Talks
Open Middle
Optimization
Pedagogy
Policy
Proof Without Words
Puzzle
Rates
Ratios & Proportions
Raw Pure Math
Regressions
Sensible?
Sidewalk Chalk
Smart Substitution
Starters
Strategy
Terminology
The Hook
The RealWorld
Topology
Understandings
VennWords
Wait. Really?
WCYDWT
What If
What is This?
What Questions
Which Would You Choose?
WODB
Yohaku
. . . View This Fullsize
Every year I give this graphic comparing the Doodle Jump stats for @ddmeyer and his friend Mike.
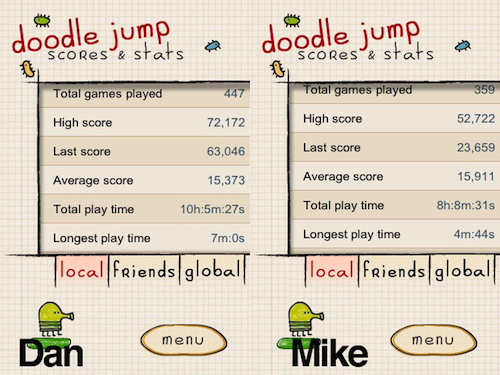
Give a couple of reasons why we could consider Dan the better player.
Give a couple of reasons why we could consider Mike the better player.
Qs? Outlier, average, max/min values, etc.
.: [STATS], [Dan Meyer], [How Many Ways?].
. . . View This Fullsize
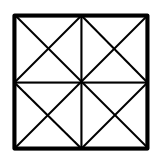
Q1: How many different ways are there to shade this to show \(\frac{1}{4}\)?
Q2: How might kids shade this to show \(\frac{1}{4}\)?
.: [PREALG], [David Wees], [How Many Ways?].
. . . View This Fullsize
The process seems to be the interesting thing here. How would you begin to work on this?
In how many ways can you write \( 2^n \) as a difference of two squares?
.: [ALG], [James Tanton], [How Many Ways?].
. . . View This Fullsize
How do you suppose we could go about finding these?
Any methods or algorithms that we might use?

Challenge: How would we determine whether this is an infinite set or a finite one?
.: [MS Math], [Erich Friedman], [How Many Ways?].
. . . View This Fullsize
In this labyrinth, there are no false turns or dead ends. You walk the line around the outside, then follow it to the middle. Assume unit distance between lines and ends of turns except for that horizontal entry line. That seems to be half a unit apart from the other lines.
What are some different ways to measure the distance walked? How might we go about that?
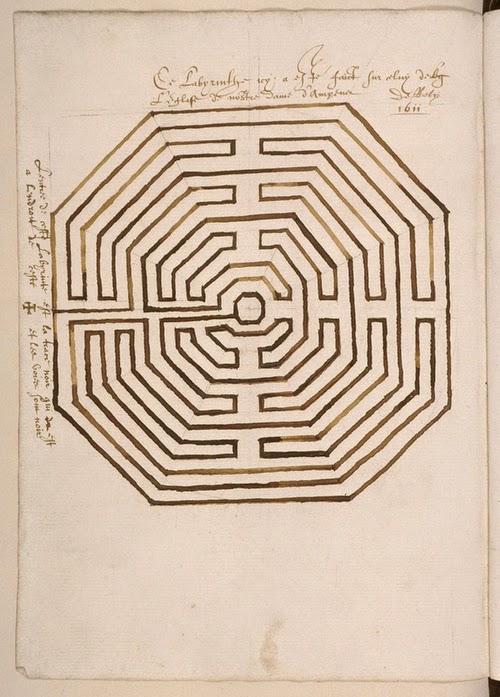
.: [LOGIC], [T.R.Milne], [How Many Ways?].
. . . View This Fullsize
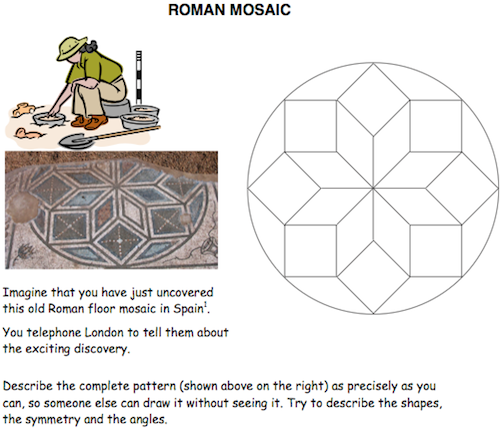
You successfully transmitted the sizes of the various figures and your correspondent has successfully created them. For a bit of fun, you say only that the final figure will be "a circumscribed polygon with more than two lines of symmetry."
How many different ways can this be accomplished ... or is that description sufficient to repeat the figure?
.: [GEOM], [Dan Meyer], [How Many Ways?].
. . . View This Fullsize
Stop the video before he starts giving out answers.
Well?
.: [MS Math], [Fawn Nguyen], [How Many Ways?].
. . . View This Fullsize
We've seen this a couple of times now.
What if I had a white marker, one that didn't show, but still held a place? How will that affect things?

.: [PROBABILTY], [internet], [How Many Ways?].
. . . View This Fullsize
Blue, green, yellow, and red ... We seem to be all set.
What if I get three black markers out of the drawer? How will that affect things?

.: [PROBABILTY], [internet], [How Many Ways?].
. . . View This Fullsize
Blue, green, yellow, and red ... We seem to be all set.
Now, what about the black, purple, and orange ones?
And BROWN!

.: [PROBABILTY], [internet], [How Many Ways?].
. . . View This Fullsize
It's a straightforward question today. Calculators are allowed for this question because we here do not feel that six-digit multiplication is worth the effort. I mean, we know you COULD do it, but that's what a tool is for, right?
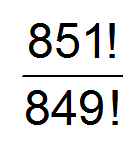
For any confused students, this problem is not suggesting that 851 is special! That's factorial notation, n!, meaning multiply the integer n by all the positive integers less than n. (Yeah, n must be a positive integer to begin with.)
For example, 6! = 6*5*4*3*2*1 = 720
For completeness, 0! = 1
.: [PRE-CALC], [internet], [How Many Ways?].