12 of 23 Items .... Type: Geometry Snacks
Problems, Questions, and Puzzles to spark discussion and argument in the maths classroom.
Navigation:
- by Source
- by Course
.... - Problem Type: 101 Things
3ACT
ASN
ChatGPT
Combinatorics
Comparisons
Constructions
Create a Problem
DebateMath
Definitions
DESMOS Art
Desmos Challenge
DoThis
Epiphany
Equity
Explainer
Find the Error
Find the Pattern
Game
Geometry Snacks
Graphicacy
Graphical Approach
How Many Ways?
How Many?
Illusion
Impossible Problem
MathArt
MathStrategy
MathTip
Meme
Mimizu
Modeling
New
New Understanding
Notation
Notice, Wonder
Number Theory
Number_Search
Number_Talks
Open Middle
Optimization
Pedagogy
Policy
Proof Without Words
Puzzle
Rates
Ratios & Proportions
Raw Pure Math
Regressions
Sensible?
Sidewalk Chalk
Smart Substitution
Starters
Strategy
Terminology
The Hook
The RealWorld
Topology
Understandings
VennWords
Wait. Really?
WCYDWT
What If
What is This?
What Questions
Which Would You Choose?
WODB
Yohaku
. . . View This Fullsize
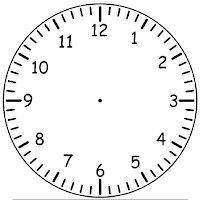
Consider a normal, everyday clock face.
If the MINUTE hand is on 2, and the hour hand and minute hand make an acute angle, what time could it be?
If the MINUTE hand is on 8, and the hour hand and minute hand make an obtuse angle, what time could it be?
.: [MS Math], [internet], [Geometry Snacks].
. . . View This Fullsize
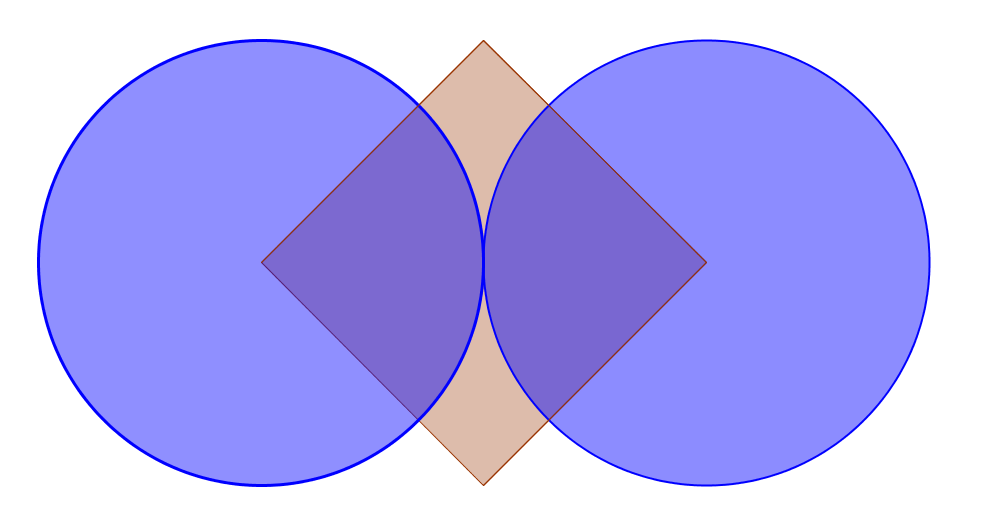
What is the red area?
The two vertices of the square are the centers of two tangent and congruent circles. If the length of a side is \( 8\sqrt{2} \), what is the area of the red part peeping out?
Here is another question: Does it matter if the circles are congruent, as long as they're tangent and the centers are at the vertices of the square?
.: [GEOM], [David Marain], [Geometry Snacks].
. . . View This Fullsize

What percent is orange? Green?
.: [PREALG], [Dan Anderson], [Geometry Snacks].
. . . View This Fullsize
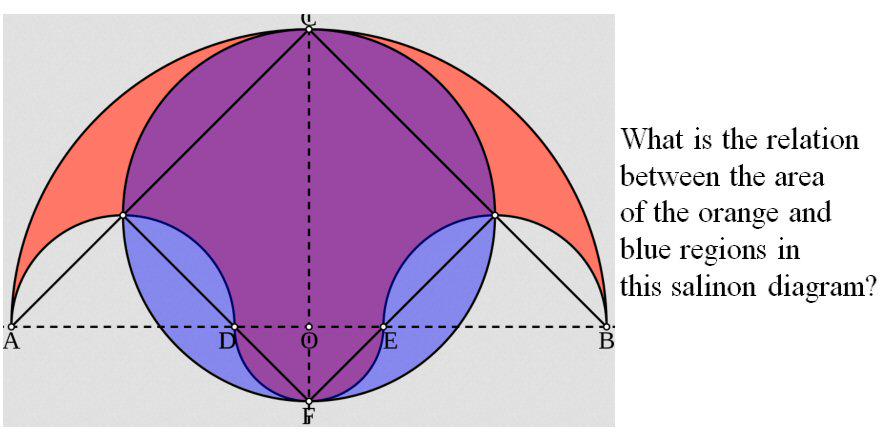
W
The Salinon was first introduced in the Book of Lemmas, a work attributed to Archimedes
.: [GEOM], [Cliff Pickover], [Geometry Snacks].
. . . View This Fullsize
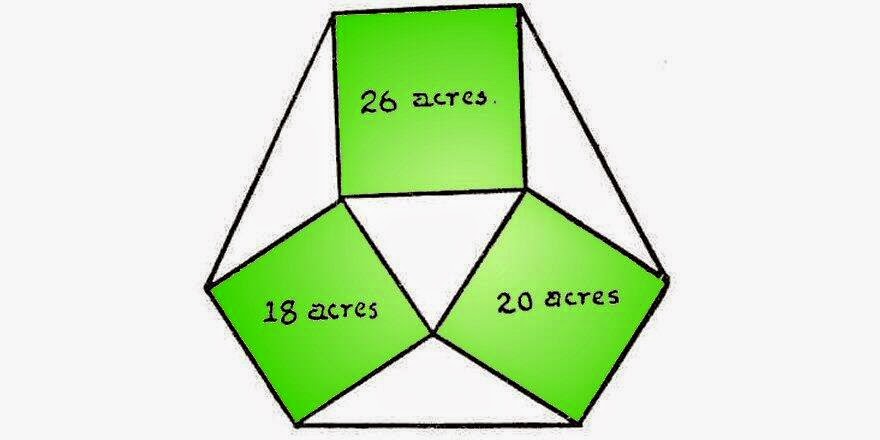
What is the area of the whole hexagonal shape?
Can your students generalize this result?
.: [GEOM], [Cliff Pickover], [Geometry Snacks].
. . . View This Fullsize
Last question with this visual:
How could you draw the inscribed semicircle (area = \( \pi \)) so that the rectangle is of maximum size?
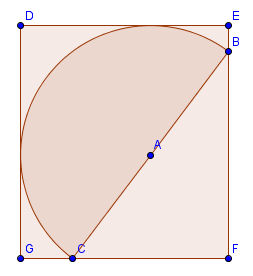
.: [GEOM], [David Marain], [Geometry Snacks].
. . . View This Fullsize
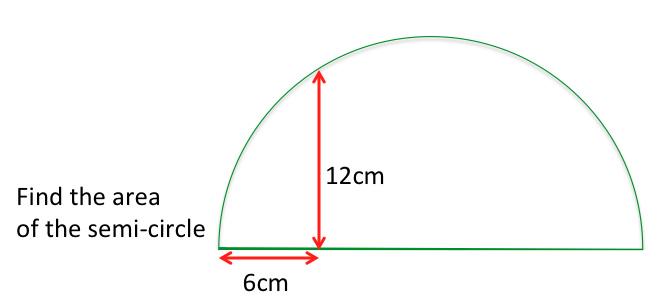
This problem was posed on Twitter the other day.
A semicircle is inscribed in a rectangle. If the area of the semicircle is pi, what's the area of the rectangle?
My question yesterday was ... how could you draw the inscribed semicircle in a way that gives a rectangle of a very different (and larger) area?
My question today is, given the arrangement below, what points did I choose that had integer coordinates? I chose a larger semicircle - for convenience - how big was it?

.: [GEOM], [David Marain], [Geometry Snacks].
. . . View This Fullsize
This problem was posed on Twitter the other day.
A semicircle is inscribed in a rectangle. If the area of the semicircle is pi, what's the area of the rectangle?
My question is ... how could you draw the inscribed semicircle in a way that gives a rectangle of a very different (and larger) area?
.: [GEOM], [David Marain], [Geometry Snacks].
. . . View This Fullsize
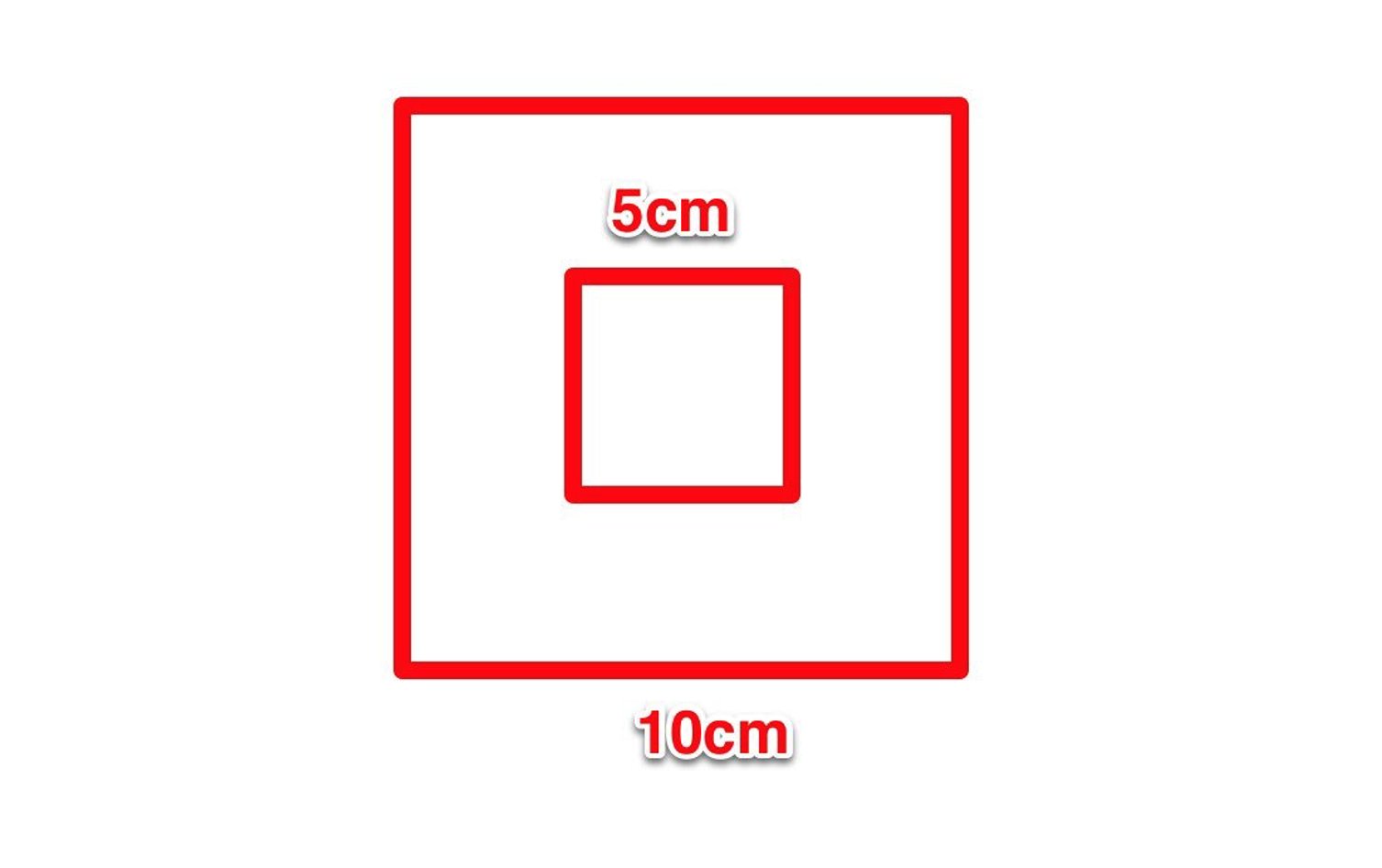
What combinations of addition or subtraction of figures could you use to find the area of the white?
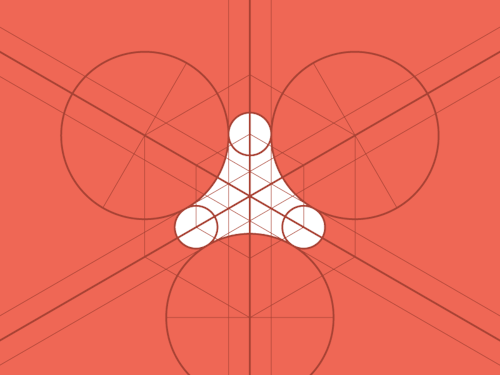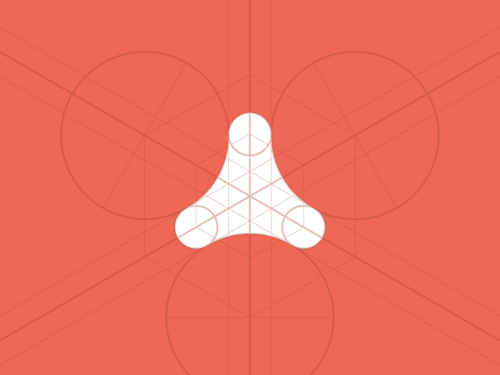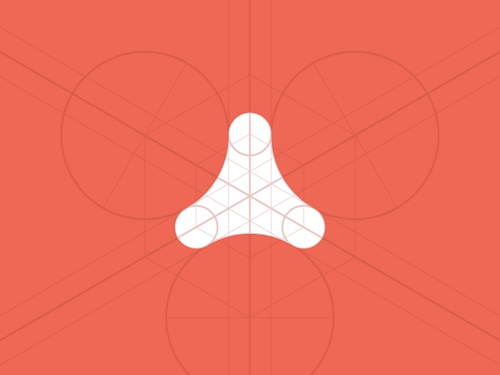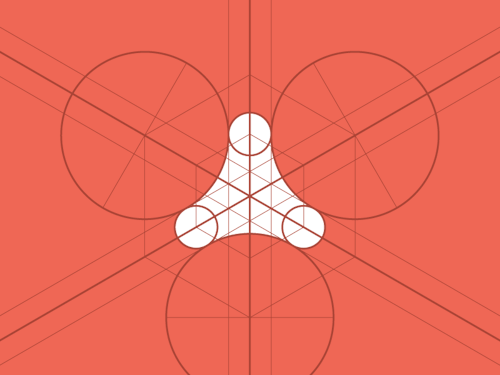
.: [GEOM], [T.R.Milne], [Geometry Snacks].
. . . View This Fullsize
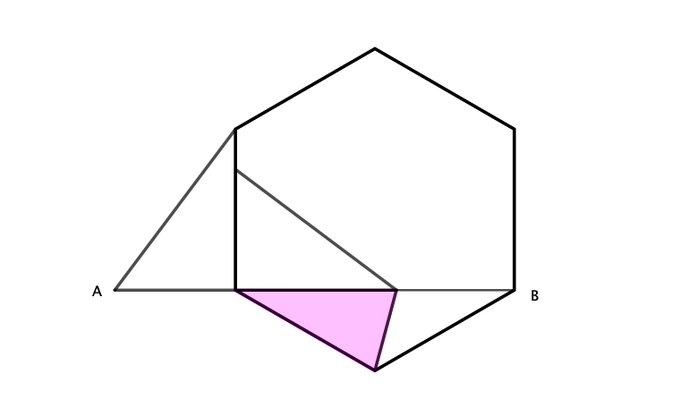
Two 3-4-5 triangles sit on straight line AB, as do 2 points that form a regular hexagon. What is the area of the pink shaded region?
.: [GEOM], [Ed Southall], [Geometry Snacks].