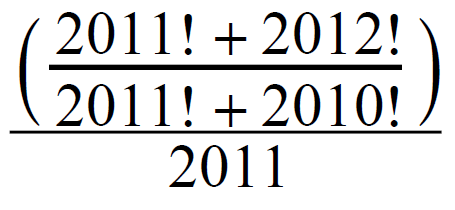10 of 10 Items .... Source: UVM
Problems, Questions, and Puzzles to spark discussion and argument in the maths classroom.
Navigation:
- by Course
- by Type
.... - Source: @yohakupuzzle
AFP
Akiyoshi Kitaoka
Aldo Bianchi
Alex Bellos
Alfie Kohn
Amanda Austin
Amie Albrecht
Avery Pickford
Ben Orlin
Benjamin Dickman
Bill Shillito
Bob Lochel
Bowman Dickson
Bryan Anderson
Catriona Agg
Cheesemonkeysf
Chris Lusto
Chris Luzniak
Cliff Pickover
Corbettmaths
Curmudgeon
Dan Anderson
Dan Draper
Dan Meyer
Dan Pearcy
Dave Richeson (@divbyzero
David Butler
David Marain
David Martin
David Wees
DESMOS
Don Steward
Dr. Pickle
Ed Southall
Elemental_41
Emma Bell
Erich Friedman
Fawn Nguyen
Five Triangles
Frank Noschese
Futility Closet
Gabriel Rosenberg
Grabarchuk
Grant Wiggins
Howie Hua
Illustrative Math
internet
James Pearce
James Tanton
Jeff Suzuki
Jennifer Wilson
Jo Morgan (@MathsJem)
Justin Aion
Kareem Carr
Kate Nowak
KHALID
Kiran Bacche
m4ths
Marco
Mary Bourassa
MathCirclesOz
MathedUp!
Mathshell
mathsjem
Matt Enlow
Megan Schmidt
Michael Pershan
Mike Lawler
Mr. Honner
Nathan Day
NCTM
Nob
NRICH
Numberphile
NYTimes
Pam Harris
Patrick Honner
PD
Poor Elijah
Quora
rawrdimus
Rhett Allain
Robert Kaplinsky
Sam Loyd
SAT
SKG
SolveMyMaths
StatSystem
Steve Phelps
Steve Wyborney
Steven Strogatz
Sunil Singh
T.R.Milne
Talking Numbers
Taylor Belcher
TickTockMath
TriangleMan
UKMT
UVM
Vi Hart
XKCD
. . . View This Fullsize
Is it possible to find a positive integer value of n so that this quotient is an integer?
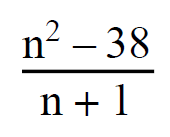
.: [ALG2], [UVM], [Find the Pattern].
. . . View This Fullsize
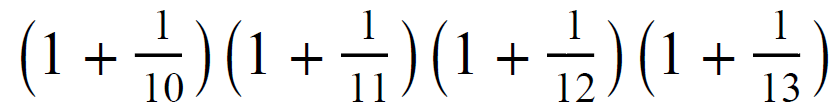
You don't need a calculator for this one either. Why not?
.: [PRE-CALC], [UVM], [Puzzle].
. . . View This Fullsize
\(log_7{\frac{1}{8}} * (log_8{25} + log_2{5}) * log_5{49} \)
Why don't we need a calculator for this problem?
.: [PRE-CALC], [UVM], [Notice, Wonder].
. . . View This Fullsize
There are 40 students in the Travel Club. They discovered that 17 members have visited Mexico, 28 have visited Canada, 10 have been to England, 12 have visited both Mexico and Canada, 3 have been only to England and 4 have been only to Mexico. Some club members have not been to any of the three foreign countries and an equal number have been to all three countries. How many students have been to all three countries?
.: [LOGIC], [UVM], [Puzzle].
. . . View This Fullsize
Two circles, radius 1 (each does not pass through the others center). All seven regions are of equal area.
What is the area of the pentagon?
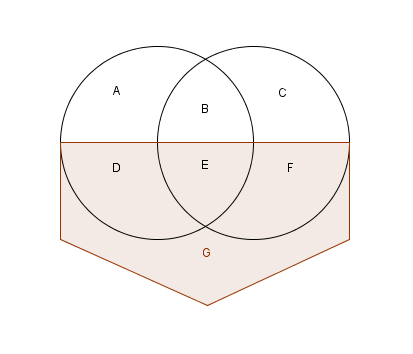
.: [GEOM], [UVM], [Notice, Wonder].
. . . View This Fullsize
What is
\(log_2 3 * log_3 4 * log_4 5 *log_5 6 * log_6 7 * log_7 8 \) ?
.: [PRE-CALC], [UVM], [Epiphany].
. . . View This Fullsize
Express the value of \(S\) as a rational number in lowest terms where
\(sin^2(10^{\circ}) + sin^2(20^{\circ}) + sin^2(30^{\circ}) +\\ sin^2(40^{\circ}) + sin^2(50^{\circ}) + sin^2(60^{\circ}) +\\ sin^2(70^{\circ}) + sin^2(80^{\circ}) + sin^2(90^{\circ}) \\ = S\)
And NO Calculator allowed.
.: [PRE-CALC], [UVM], [Raw Pure Math].
. . . View This Fullsize
The test is designed for 11th/12th, Precalculus or above. There's 41 questions. No calculators, tech, or references. Pencil & paper only.
and just TWO HOURS.
Average precalculus students can get 10/41 in the allotted time, really good ones about 20/41, exceptional ones 25-30.
Since there's no calculators, all the questions must be solvable with only pencil/paper (duh). That combined with "rational number in lowest terms" means there's a clever insight needed, a step that changes the imposing to manageable. That's what I like about them.
INSTRUCTIONS:
CALCULATORS, COMPUTERS AND/OR ANY OTHER ELECTRONIC DEVICES ARE NOT PERMITTED.
UNLESS OTHERWISE INDICATED, ALL ANSWERS MUST BE EXPRESSED IN SIMPLEST FORM.
A radical expression of index \(n\) is in simplest form if the radicand is not a fraction, denominators are rationalized and integer radicands do not have any factors that are \(n\)th powers of a prime. For example, \(\sqrt{\frac{5}{12}}\) simplifies to \(\frac{\sqrt{15}}{6} \)
Do NOT approximate the number π.
Do NOT approximate radicals.
Logarithms: The notation \(\log \) is logarithm to the base 10. The notation \(\log_a\) is logarithm to the base a. The notation LN is logarithm to the base e.
The symbol ! is the factorial symbol. For example, 3! = 3∙2∙1 = 6.
The symbol i is the complex unit \(\sqrt{-1}\)
All numbers are in base 10 unless otherwise indicated (e.g., \(1001_2\) is the base 2 representation of the decimal number 9).
Any answer which is a nonintegral rational number must be expressed in the form \(\frac{a}{b}\), where a and b are integers that have no common divisor other than 1.
.: [PRE-CALC], [UVM], [Puzzle].