11 of 11 Items .... Source: Matt Enlow
Problems, Questions, and Puzzles to spark discussion and argument in the maths classroom.
Navigation:
- by Course
- by Type
.... - Source: @yohakupuzzle
AFP
Akiyoshi Kitaoka
Aldo Bianchi
Alex Bellos
Alfie Kohn
Amanda Austin
Amie Albrecht
Avery Pickford
Ben Orlin
Benjamin Dickman
Bill Shillito
Bob Lochel
Bowman Dickson
Bryan Anderson
Catriona Agg
Cheesemonkeysf
Chris Lusto
Chris Luzniak
Cliff Pickover
Corbettmaths
Curmudgeon
Dan Anderson
Dan Draper
Dan Meyer
Dan Pearcy
Dave Richeson (@divbyzero
David Butler
David Marain
David Martin
David Wees
DESMOS
Don Steward
Dr. Pickle
Ed Southall
Elemental_41
Emma Bell
Erich Friedman
Fawn Nguyen
Five Triangles
Frank Noschese
Futility Closet
Gabriel Rosenberg
Grabarchuk
Grant Wiggins
Howie Hua
Illustrative Math
internet
James Pearce
James Tanton
Jeff Suzuki
Jennifer Wilson
Jo Morgan (@MathsJem)
Justin Aion
Kareem Carr
Kate Nowak
KHALID
Kiran Bacche
m4ths
Marco
Mary Bourassa
MathCirclesOz
MathedUp!
Mathshell
mathsjem
Matt Enlow
Megan Schmidt
Michael Pershan
Mike Lawler
Mr. Honner
Nathan Day
NCTM
Nob
NRICH
Numberphile
NYTimes
Pam Harris
Patrick Honner
PD
Poor Elijah
Quora
rawrdimus
Rhett Allain
Robert Kaplinsky
Sam Loyd
SAT
SKG
SolveMyMaths
StatSystem
Steve Phelps
Steve Wyborney
Steven Strogatz
Sunil Singh
T.R.Milne
Talking Numbers
Taylor Belcher
TickTockMath
TriangleMan
UKMT
UVM
Vi Hart
XKCD
. . . View This Fullsize
On a square lattice, a circle can pass through 2, 3, or 4 points, as in the diagram below. The original question asks for a circle that passes through 5 points, but can you define a circle that passes through other numbers of points? and explain how the circle was created?
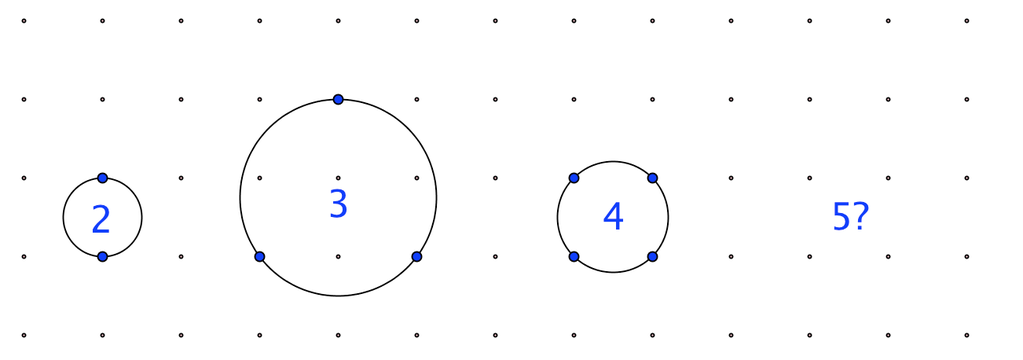
.: [GEOM], [Matt Enlow], [Puzzle].
. . . View This Fullsize
Sam Shah wrote:
Matt Enlow (math teacher in MA) posted a fascinating problem online today, one he thinks of when storing all those plastic bags from the grocery store. You shove them so they all lie in a single bag, and throw that bag under the sink. Here’s the question: how many different ways can you store these bags?
For 1 bag, there is only 1 way.
For 2 bags, there is still only 1 way.
For 3 bags, there are 2 ways.
Here is a picture for clarification:
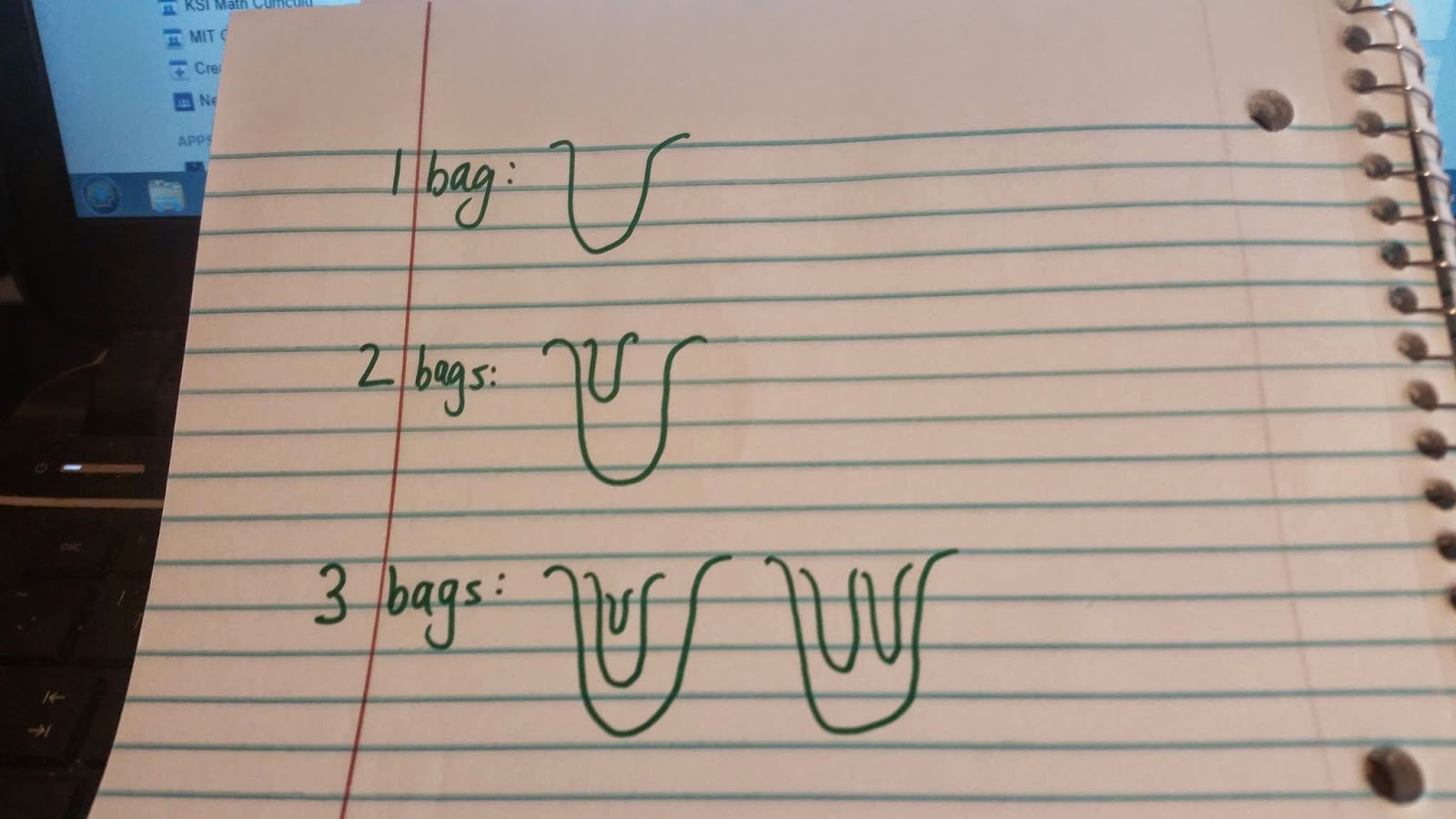
Can you figure out how many ways for 6 bags? 13 bags?
.: [LOGIC], [Matt Enlow], [Find the Pattern].
. . . View This Fullsize
If it takes me 60 minutes to cook dinner by myself, and 90 minutes if one of my kids is "helping" me, how long would it take her to do it herself?
.: [PREALG], [Matt Enlow], [Notice, Wonder].
. . . View This Fullsize
Which infinite sum is greater?
\(\frac{1}{2} + \frac{2}{4} + \frac{3}{8} + \frac{4}{16} + \frac{5}{32} + \frac{6}{64} + \frac{7}{128} ... \)
or
\(\frac{1}{2} + \frac{1}{4} + \frac{2}{8} + \frac{3}{16} + \frac{5}{32} + \frac{8}{64} + \frac{13}{128} ...\)
.: [ALL], [Matt Enlow], [Notice, Wonder].
. . . View This Fullsize
\(\frac{1}{4} + \frac{1}{8} + \frac{2}{16} + \frac{3}{32} + \frac{5}{64} + \frac{8}{128} + \frac{13}{256} + \frac{21}{512} + \frac{34}{1024} + ...\)
.: [PRE-CALC], [Matt Enlow], [Puzzle].
. . . View This Fullsize
Can complex numbers be categorized into rational and irrational, or is it only the real numbers that get divided that way? What do you think about this idea?
Must irrational numbers be real? If you think so, how do you reconcile the various definitions of irrational?
If you don't think so, why do we seem to perpetuate this idea with students that irrationals are composed entirely in the real number system...perhaps not by stating that directly, but by using representations such as the ones below?
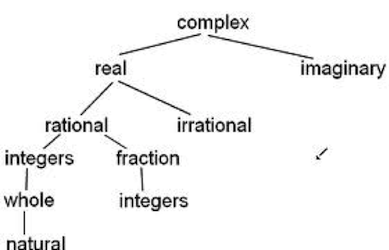
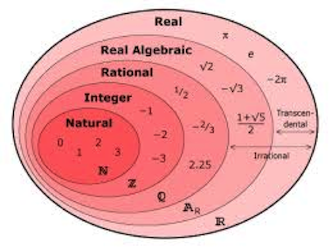
This next is an extra credit project for a college teacher prep program ... these students obviously don't know their subject all that well and this "teacher" is no better. "Hands On Math: Burn The Textbooks, Shred The Worksheets, Teach Math." is the blog motto.

3
Are the visual organizers getting in the way of the understanding?
.: [ALL], [Matt Enlow], [Understandings].
. . . View This Fullsize
Is this the largest parabolic segment that can fit in a square?
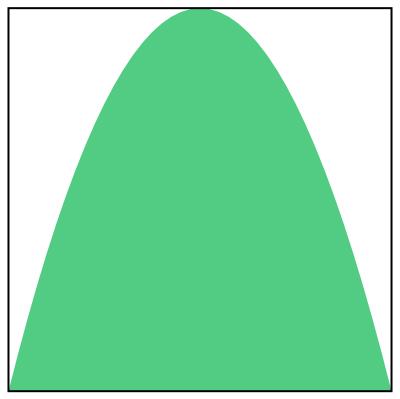
... You sure this one isn't just a little bit larger?
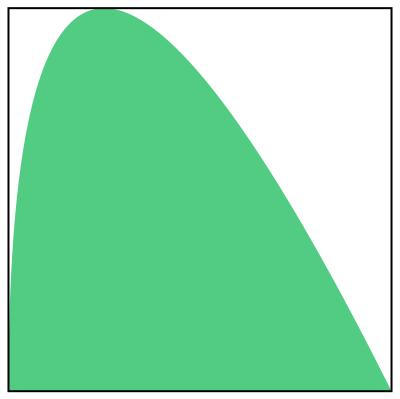
.: [PRE-CALC], [Matt Enlow], [Comparisons].
. . . View This Fullsize
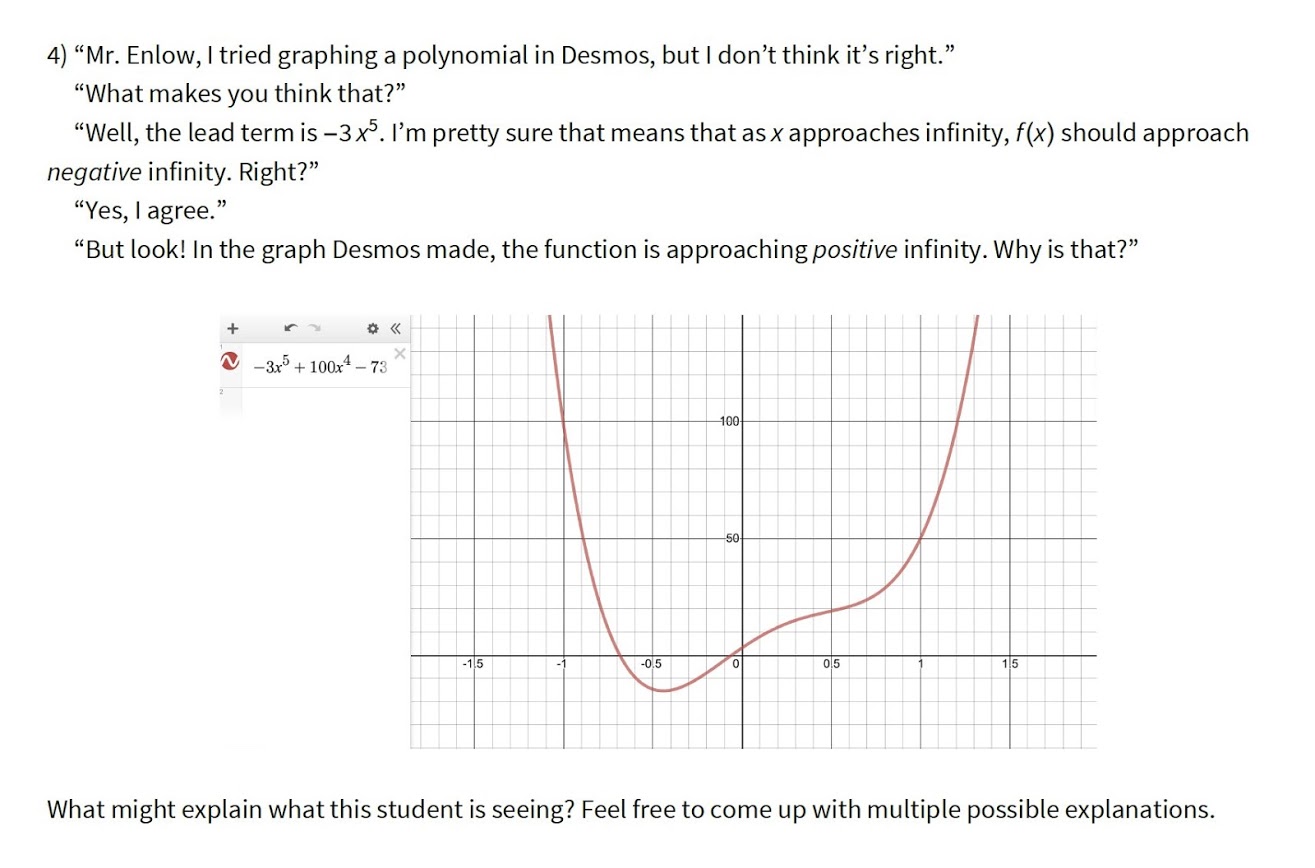
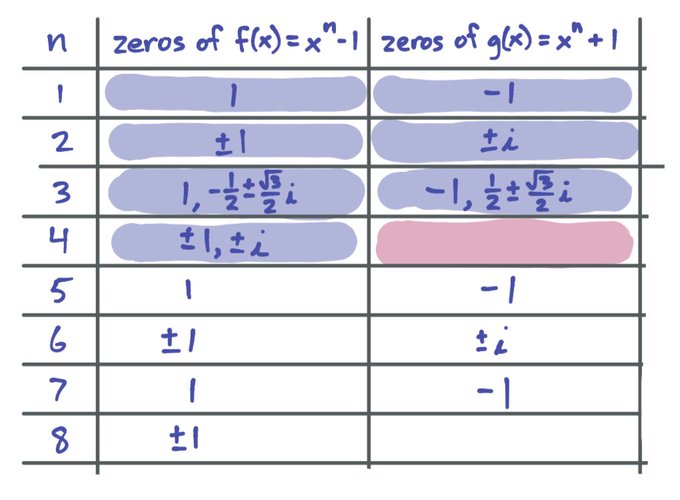
In Algebra 2 Honors, we spent 45 minutes trying to fill out this table as much as we could. It was awesome. Left them with a nice cliffhanger to ponder over Thanksgiving: What are the zeros of \(x^4+1\)?
.: [PRE-CALC], [Matt Enlow], [Epiphany].
. . . View This Fullsize
How many quadratic trinomials \(q(x)\) can you find such that both \( q(x) \) and \( q(x) + 1\) are factorable into two binomials?
#WonderWithMe
.: [ALG2], [Matt Enlow], [How Many?].