6 of 6 Items .... Source: Kate Nowak
Problems, Questions, and Puzzles to spark discussion and argument in the maths classroom.
Navigation:
- by Course
- by Type
.... - Source: @yohakupuzzle
AFP
Akiyoshi Kitaoka
Aldo Bianchi
Alex Bellos
Alfie Kohn
Amanda Austin
Amie Albrecht
Avery Pickford
Ben Orlin
Benjamin Dickman
Bill Shillito
Bob Lochel
Bowman Dickson
Bryan Anderson
Catriona Agg
Cheesemonkeysf
Chris Lusto
Chris Luzniak
Cliff Pickover
Corbettmaths
Curmudgeon
Dan Anderson
Dan Draper
Dan Meyer
Dan Pearcy
Dave Richeson (@divbyzero
David Butler
David Marain
David Martin
David Wees
DESMOS
Don Steward
Dr. Pickle
Ed Southall
Elemental_41
Emma Bell
Erich Friedman
Fawn Nguyen
Five Triangles
Frank Noschese
Futility Closet
Gabriel Rosenberg
Grabarchuk
Grant Wiggins
Howie Hua
Illustrative Math
internet
James Pearce
James Tanton
Jeff Suzuki
Jennifer Wilson
Jo Morgan (@MathsJem)
Justin Aion
Kareem Carr
Kate Nowak
KHALID
Kiran Bacche
m4ths
Marco
Mary Bourassa
MathCirclesOz
MathedUp!
Mathshell
mathsjem
Matt Enlow
Megan Schmidt
Michael Pershan
Mike Lawler
Mr. Honner
Nathan Day
NCTM
Nob
NRICH
Numberphile
NYTimes
Pam Harris
Patrick Honner
PD
Poor Elijah
Quora
rawrdimus
Rhett Allain
Robert Kaplinsky
Sam Loyd
SAT
SKG
SolveMyMaths
StatSystem
Steve Phelps
Steve Wyborney
Steven Strogatz
Sunil Singh
T.R.Milne
Talking Numbers
Taylor Belcher
TickTockMath
TriangleMan
UKMT
UVM
Vi Hart
XKCD
. . . View This Fullsize
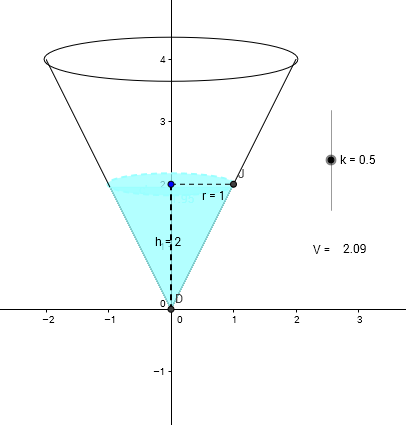
The last of the three related-rate geogebra problems from Kate Nowak. It's the related rate problem from calculus: the conical tank being filled with water.
Adjust the slider and... wait, what is changing and how?
For every click of the slider:
Is the depth increasing at a constant rate?
Is the radius increasing at a constant rate?
Is the volume increasing at a constant rate?
How can you tell?
- Where or how, in the RealWorldtm, could we see the constant increase in volume?
- Where or how, in the RealWorldtm, could we see the constant increase in radius, or depth?
.: [CALC], [Kate Nowak], [Explainer].
. . . View This Fullsize

We've all seen this problem, but many of our students haven't. It's the related rate problem from calculus: the balloon being filled with air.
There are two questions being demonstrated here.
(1) "If the volume increases at a constant rate, what is happening to the radius?" and
(2) "If the radius increases at a constant rate, what is happening to the volume?"
The first question is to figure out which situation is modeled in red and which in blue.
Then we can ask:
- Does the radius increase at a constant speed in both models? How can you tell?
- Does the volume increase at a constant speed in both models? How can you tell?
- Where or how, in the RealWorldtm, could we see the constant increase in volume?
- Where or how, in the RealWorldtm, could we see the constant increase in radius?
.: [CALC], [Kate Nowak], [Comparisons].
. . . View This Fullsize
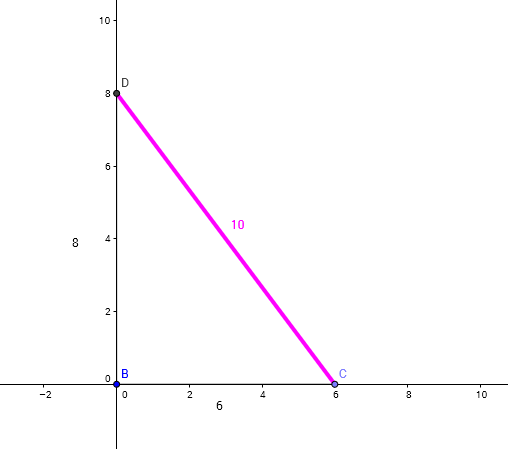
We've all seen this problem, but many of our students haven't.
It's the related rate problem from calculus: the ladder sliding down the wall.
The "official" question?
How fast is the ladder's top sliding down the wall if the bottom is being pulled out at a rate of 1 ft/sec?
We can ask a few questions of kids at any level, though, based on the given that the bottom of the ladder is being pulled to the right at 1 foot per sec.
- Does the top drop at a constant speed?
- Does the top drop a distance equal to the horizontal movement?
- When is the speed of the top greater than 1, less than 1, and equal to 1?
- If this is a 25 foot ladder, with the bottom 7 feet out from the base of the wall, and the top drops 4 feet ... how far out does the bottom of the ladder have to go?
.: [CALC], [Kate Nowak], [Understandings].
. . . View This Fullsize
\( x^2 = 81 \) has two solutions, -9 and 9.
But does \( \sqrt{81} \) have one solution or two?
Is it correct to say that \( \sqrt{81} \) = +9 and -9?
Or should we be saying that \( \sqrt{81} \) is an expression and that \( 9\), \(\frac{18}{2} \), \(27^{2/3} \), and \(1+6+2\), are equivalent expressions?
.: [ALG1], [Kate Nowak], [Understandings].
. . . View This Fullsize
Are these the same or not the same? Why? (What makes them different if you think they're different?)
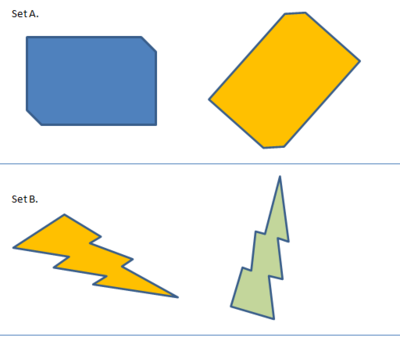
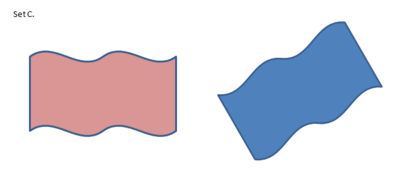
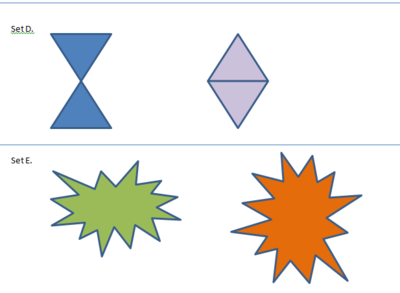

.: [GEOM], [Kate Nowak], [Notice, Wonder].
. . . View This Fullsize
Can you show if this is true?
\(2^6 * 2^6 = 2^{11} + 2^{11}\)
Can we generate more like this one ... simple and elegant?
How about one with 3 as a base?
.: [ALG], [Kate Nowak], [Explainer].