12 of 25 Items .... Source: James Tanton

Ask your class if there are any Pythagorean anti-Triples: \(\dfrac{1}{a^2} + \dfrac{1}{b^2} = \dfrac{1}{c^2}\) ?

If a, b, c are integers, the question seems harder, since 1/3, 1/4, 1/5 would be (to me) obvious answers - leading to the rules for Pythagorean triples and just using their reciprocals.

.: [ALG1], [James Tanton], [Epiphany].

. . . View This Fullsize

We all recognize the Fibonacci Sequence: 1, 1, 2, 3, 5, 8, 13, 21, ...
What is the units digit of the sixty-first Fibonacci number?

Is there a pattern?

.: [ALL], [James Tanton], [Number Theory].

. . . View This Fullsize

Let's examine the function g(n):

g(n) = smallest integer such that g(n)*n! is a perfect square.

How should we go about finding if there's a pattern in that?

.: [PRE-CALC], [James Tanton], [Raw Pure Math].

. . . View This Fullsize

Equilateral triangles tile the plane. Is it possible to select four intersection points that are the corners of a perfect square?

.: [GEOM], [James Tanton], [Strategy].

. . . View This Fullsize

5 distinct numbers are chosen at random from {1,2,3,4,5,6,7,8,9}.

p(k) = probability their sum = k.

What are some of the ways you can find this in general?
What sum is/are the least likely?
Which sum is/are most likely?

p(15)=?

p(35)=?

.: [PROBABILTY], [James Tanton], [Raw Pure Math].

. . . View This Fullsize

The process seems to be the interesting thing here. How would you begin to work on this?

In how many ways can you write \( 2^n \) as a difference of two squares?

.: [ALG], [James Tanton], [How Many Ways?].

. . . View This Fullsize

Find two polynomials whose four points of intersection form a perfect square. (...with integer coefficients?)

What's the best way to do that?

.: [PRE-CALC], [James Tanton], [Raw Pure Math].

. . . View This Fullsize

.: [LOGIC], [James Tanton], [Proof Without Words].

. . . View This Fullsize

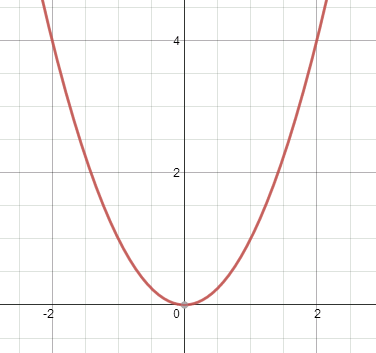
Is it possible to choose four points on the graph of y = x² that are the vertices of a trapezoid?

A parallelogram?

An equilateral triangle?

Here's \(y = x^2\) to help you think.

.: [PRE-CALC], [James Tanton], [Number Theory].

. . . View This Fullsize

After yesterday, I have to ask ... Is there a largest odd number that is not the sum of three composite odd numbers?

— James Tanton (@jamestanton)

.: [ALL], [James Tanton], [Number Theory].

. . . View This Fullsize

What is the largest even integer that cannot be written as the sum of two odd composite numbers?

R1
For example, 42 = 21 + 21, so it is not a candidate. 22 is a candidate because no pair of 9, 15, or 21 can equal 22.

As with many of Mr. Tanton's puzzles, there's a way to know that you are absolutely correct. Can you find the number and the explanation?

.: [ALL], [James Tanton], [New Understanding].

. . . View This Fullsize

If you've ever played with a Rubic's Cube, you know it's possible to divide a cube into 27 smaller cubes. Eight and sixty-four is pretty obvious, too.

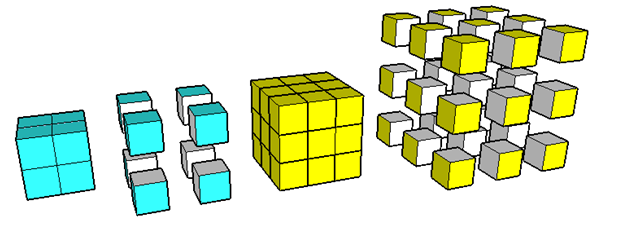
Can you show how to divide a cube into other numbers of sub-cubes, numbers that aren't perfect cubic numbers?

Like 15? or 20?

Because you don't have enough awesome in your life, I present watermelon cubes.

.: [ALL], [James Tanton], [Epiphany].