12 of 16 Items .... Source: Grant Wiggins
Problems, Questions, and Puzzles to spark discussion and argument in the maths classroom.
Navigation:
- by Course
- by Type
.... - Source: @yohakupuzzle
AFP
Akiyoshi Kitaoka
Aldo Bianchi
Alex Bellos
Alfie Kohn
Amanda Austin
Amie Albrecht
Avery Pickford
Ben Orlin
Benjamin Dickman
Bill Shillito
Bob Lochel
Bowman Dickson
Bryan Anderson
Catriona Agg
Cheesemonkeysf
Chris Lusto
Chris Luzniak
Cliff Pickover
Corbettmaths
Curmudgeon
Dan Anderson
Dan Draper
Dan Meyer
Dan Pearcy
Dave Richeson (@divbyzero
David Butler
David Marain
David Martin
David Wees
DESMOS
Don Steward
Dr. Pickle
Ed Southall
Elemental_41
Emma Bell
Erich Friedman
Fawn Nguyen
Five Triangles
Frank Noschese
Futility Closet
Gabriel Rosenberg
Grabarchuk
Grant Wiggins
Howie Hua
Illustrative Math
internet
James Pearce
James Tanton
Jeff Suzuki
Jennifer Wilson
Jo Morgan (@MathsJem)
Justin Aion
Kareem Carr
Kate Nowak
KHALID
Kiran Bacche
m4ths
Marco
Mary Bourassa
MathCirclesOz
MathedUp!
Mathshell
mathsjem
Matt Enlow
Megan Schmidt
Michael Pershan
Mike Lawler
Mr. Honner
Nathan Day
NCTM
Nob
NRICH
Numberphile
NYTimes
Pam Harris
Patrick Honner
PD
Poor Elijah
Quora
rawrdimus
Rhett Allain
Robert Kaplinsky
Sam Loyd
SAT
SKG
SolveMyMaths
StatSystem
Steve Phelps
Steve Wyborney
Steven Strogatz
Sunil Singh
T.R.Milne
Talking Numbers
Taylor Belcher
TickTockMath
TriangleMan
UKMT
UVM
Vi Hart
XKCD
. . . View This Fullsize
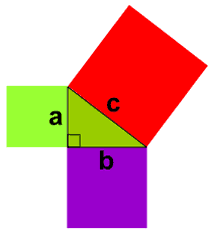
Pythagorean theorem: \(a^2 +b^2 = c^2\)
“In a right triangle, the area of the square drawn on the hypotenuse is equal to the sum of the areas of the squares drawn on the other two legs.”
Here is the problem: does the figure whose areas we compare, drawn on the triangle's legs, have to be square?
Can there be other shapes – triangles, rhombuses, regular pentagons, etc. – that make the Pythagorean Theorem more generally true?
.: [ALL], [Grant Wiggins], [New Understanding].
. . . View This Fullsize

Question 15: Negative times a negative is ... ?
Why is a negative times a negative equal to a positive?
.: [ALL], [Grant Wiggins], [Explainer].
. . . View This Fullsize
True or false? .999999… = 1
To the best of your understanding, explain why you think so.
.: [ALL], [Grant Wiggins], [Explainer].
. . . View This Fullsize
“In geometry we assume many axioms.”
To the best of your understanding, explain the difference between valid and goofy axioms. What gives us the right to assume the axioms we do in Euclidean geometry?
.: [ALL], [Grant Wiggins], [Explainer].
. . . View This Fullsize
“In geometry, we begin with undefined terms.”
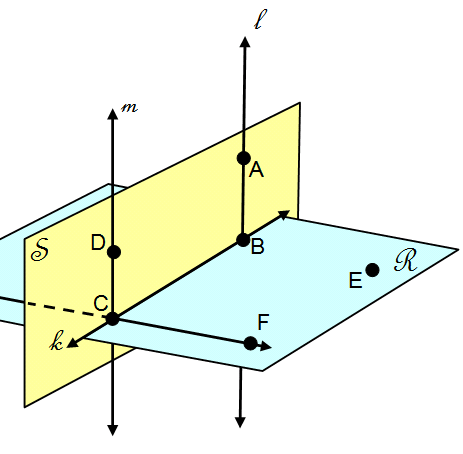
Here’s what’s odd, though: every Geometry textbook always draws points, lines, and planes in exactly the same familiar and obvious way – as if we CAN define them, at least visually.
To the best of your understanding, define “undefined term” and explain why it doesn’t mean that points and lines have to be drawn the way we draw them; nor does it mean, on the other hand, that math chaos will ensue if there are no definitions or familiar images for the basic elements.
.: [ALL], [Grant Wiggins], [Explainer].
. . . View This Fullsize
There's an “accurate” answer and “an appropriately precise” answer.
To the best of your understanding, explain the difference between an “accurate” answer and “an appropriately precise” answer.
(HINT: when is the answer on your calculator inappropriate?)
.: [ALL], [Grant Wiggins], [Explainer].
. . . View This Fullsize

As you know, PEMDAS is shorthand for the order of operations for evaluating complex expressions (Parentheses, then Exponents, etc.).
The order of operations is a convention.
X(A + B) = XA + XB is the distributive property. It is a law.
To the best of your understanding, explain the difference between a convention and a law. Give another example of each.
.: [ALL], [Grant Wiggins], [Explainer].
. . . View This Fullsize

Why were imaginary numbers invented?
12th graders: Why was the calculus invented?
.: [ALL], [Grant Wiggins], [Explainer].
. . . View This Fullsize
Create the equations that a website or a calculator might use to convert between feet and yards. What are the equations that describe the mathematical relationship?
HINT: all you need as parts of the equation are F, Y, =, and 3.
.: [ALL], [Grant Wiggins], [Explainer].
. . . View This Fullsize

Most teachers assign final grades by using the mathematical mean (the “average”) to determine them, but this measure hides information. What information is hidden and what, if anything, should we do about it?
To the best of your understanding, explain what the mean hides and give at least two reasons why the mean may not be the best measure of achievement.
.: [ALL], [Grant Wiggins], [Explainer].
. . . View This Fullsize

A catering company rents out tables for big parties. 8 people can sit around a table. A school is giving a party for parents, siblings, students and teachers. The guest list totals 243. How many tables should the school rent?
Explain your logic.
.: [ALL], [Grant Wiggins], [Explainer].
. . . View This Fullsize
“Multiplication is just repeated addition.”
To the best of your understanding, explain why this statement is false, giving examples.
.: [ALL], [Grant Wiggins], [Explainer].