12 of 45 Items .... Source: David Marain

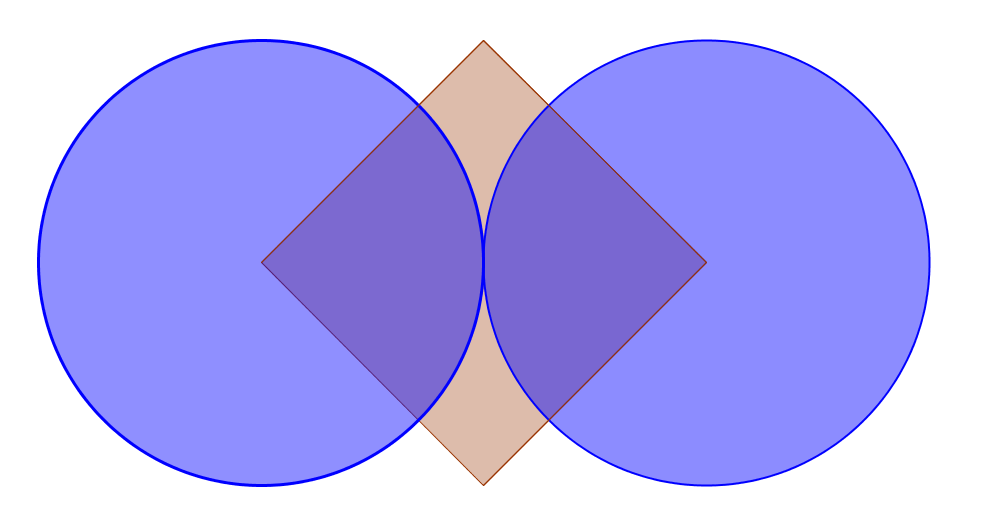
What is the red area?

The two vertices of the square are the centers of two tangent and congruent circles. If the length of a side is \( 8\sqrt{2} \), what is the area of the red part peeping out?

Here is another question: Does it matter if the circles are congruent, as long as they're tangent and the centers are at the vertices of the square?

.: [GEOM], [David Marain], [Geometry Snacks].

. . . View This Fullsize

If we stipulate that

\( (x+12)^2+(y+4)^2+(z+3)^2=0\), then

\( \sqrt{x^2+y^2+z^2}=?\)

Should we brute-force this or is there a more beautiful or subtle way of getting what we want?

.: [PRE-CALC], [David Marain], [Raw Pure Math].

. . . View This Fullsize

Population of organism after n minutes is \(P(n) = k*9^{(\frac{n}{2})}\).

What is the growth factor?
... algebraically stated, what is the ratio of P(t+1):P(t)?

.: [ALG2], [David Marain], [Find the Pattern].

. . . View This Fullsize

The sum of \(\frac{1}{4}\) and a number is equal to the product of \(\frac{1}{4}\) and the number.

(a) Explain why the number must be negative.

(b) What's the number ?

.: [ALG1], [David Marain], [Explainer].

. . . View This Fullsize

For how many integers k is \(10,000 - k^2\) positive?

.: [ALL], [David Marain], [Number Theory].

. . . View This Fullsize

Last question with this visual:

How could you draw the inscribed semicircle (area = \( \pi \)) so that the rectangle is of maximum size?

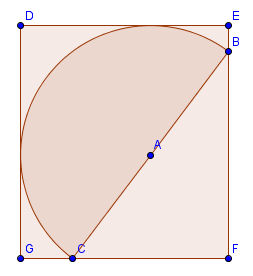
.: [GEOM], [David Marain], [Geometry Snacks].

. . . View This Fullsize

This problem was posed on Twitter the other day.

A semicircle is inscribed in a rectangle. If the area of the semicircle is pi, what's the area of the rectangle?

My question yesterday was ... how could you draw the inscribed semicircle in a way that gives a rectangle of a very different (and larger) area?

My question today is, given the arrangement below, what points did I choose that had integer coordinates? I chose a larger semicircle - for convenience - how big was it?

.: [GEOM], [David Marain], [Geometry Snacks].

. . . View This Fullsize

This problem was posed on Twitter the other day.

A semicircle is inscribed in a rectangle. If the area of the semicircle is pi, what's the area of the rectangle?

My question is ... how could you draw the inscribed semicircle in a way that gives a rectangle of a very different (and larger) area?

.: [GEOM], [David Marain], [Geometry Snacks].

. . . View This Fullsize

Which mental path do you think is easiest for beginning students? (Analytical, numerical, graphical, algebraic?) Would you give a different hint to beginning students than to advanced students?

Will the average of \( 2^{48} \) & \( 2^{50}\) be less than, greater than, or equal to \( 2^{49} \)?

Can you find the actual average? (without a calculator!)

.: [SAT], [David Marain], [Number Theory].

. . . View This Fullsize

If a and b are both positive integers, \(a^{a - b}=10^6\),
list all possible ordered pairs (a,b).

What are a couple of different ways to approach this nugget?

What are the "obvious" answers that everyone will miss?

.: [ALG2], [David Marain], [Raw Pure Math].

. . . View This Fullsize

Imagine a cube, 2 inches on a side ...

Actually, don't bother, I'll put one over there on the right side. ==>>

Now imagine if you were sitting on a vertex. How far is it (straight line distance) to the other vertices?

How many of those paths would be rational number distances?

What if you were on the midpoint of an edge and considering the paths to the vertices again. How many of those paths would have rational lengths distances?

And, no, I won't apologize for the pun. Pfft!

.: [MS Math], [David Marain], [Puzzle].