9 of 9 Items .... Source: David Butler
Problems, Questions, and Puzzles to spark discussion and argument in the maths classroom.
Navigation:
- by Course
- by Type
.... - Source: @yohakupuzzle
AFP
Akiyoshi Kitaoka
Aldo Bianchi
Alex Bellos
Alfie Kohn
Amanda Austin
Amie Albrecht
Avery Pickford
Ben Orlin
Benjamin Dickman
Bill Shillito
Bob Lochel
Bowman Dickson
Bryan Anderson
Catriona Agg
Cheesemonkeysf
Chris Lusto
Chris Luzniak
Cliff Pickover
Corbettmaths
Curmudgeon
Dan Anderson
Dan Draper
Dan Meyer
Dan Pearcy
Dave Richeson (@divbyzero
David Butler
David Marain
David Martin
David Wees
DESMOS
Don Steward
Dr. Pickle
Ed Southall
Elemental_41
Emma Bell
Erich Friedman
Fawn Nguyen
Five Triangles
Frank Noschese
Futility Closet
Gabriel Rosenberg
Grabarchuk
Grant Wiggins
Howie Hua
Illustrative Math
internet
James Pearce
James Tanton
Jeff Suzuki
Jennifer Wilson
Jo Morgan (@MathsJem)
Justin Aion
Kareem Carr
Kate Nowak
KHALID
Kiran Bacche
m4ths
Marco
Mary Bourassa
MathCirclesOz
MathedUp!
Mathshell
mathsjem
Matt Enlow
Megan Schmidt
Michael Pershan
Mike Lawler
Mr. Honner
Nathan Day
NCTM
Nob
NRICH
Numberphile
NYTimes
Pam Harris
Patrick Honner
PD
Poor Elijah
Quora
rawrdimus
Rhett Allain
Robert Kaplinsky
Sam Loyd
SAT
SKG
SolveMyMaths
StatSystem
Steve Phelps
Steve Wyborney
Steven Strogatz
Sunil Singh
T.R.Milne
Talking Numbers
Taylor Belcher
TickTockMath
TriangleMan
UKMT
UVM
Vi Hart
XKCD
. . . View This Fullsize
What do you think of this method of completing the square?
Prof Butler likes it because you can go direct from factored form to vertex form.
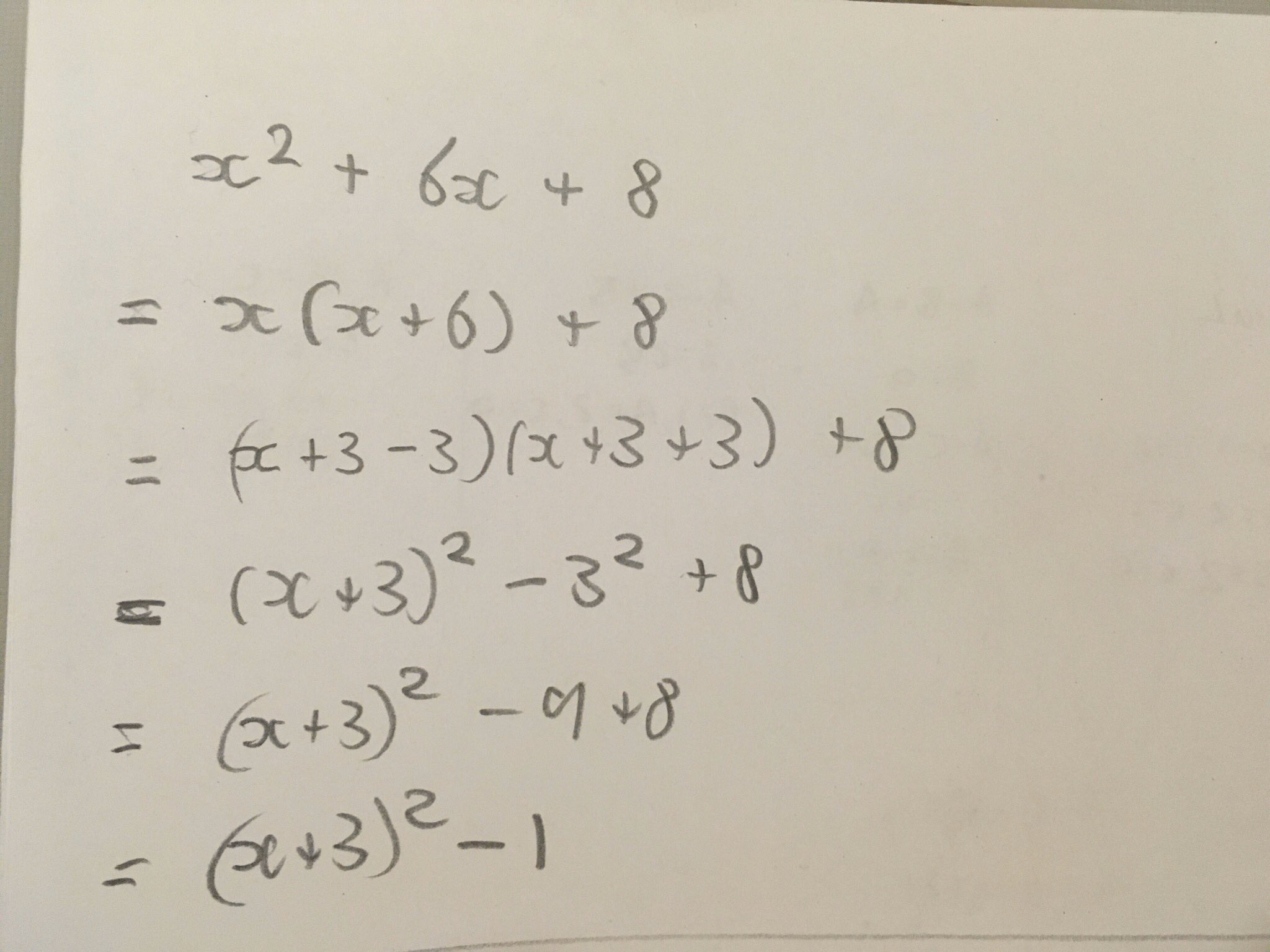
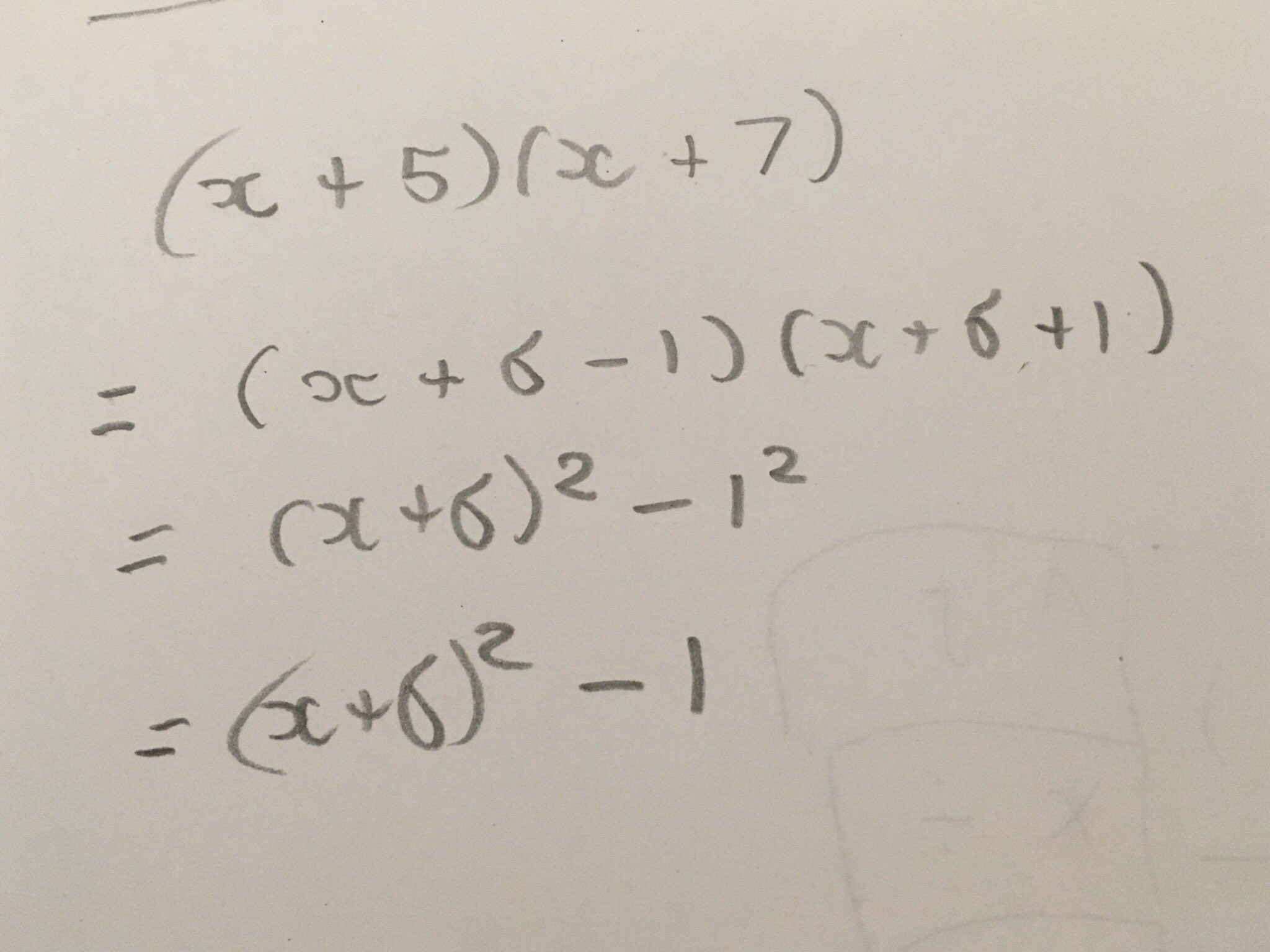
\( x^2 + 12x + 35 \)
\( = x(x + 12) + 35 \)
\( = (x + 6 - 6)(x + 6 + 6) + 35 \)
\( = (x + 6)^2 - 36 + 35 \)
\( = (x + 6)^2 - 1 \)
How does the special factoring of \(a^2 - b^2 \) come into all of this?
.: [ALG2], [David Butler], [New Understanding].
. . . View This Fullsize
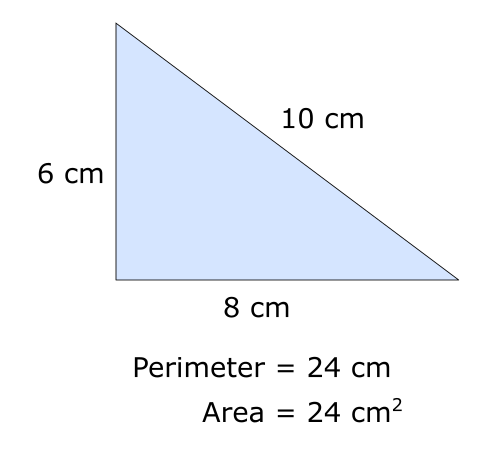
Some triangles have the same perimeter in \(cm\) as area in \(cm^2\), like the 6cm-8cm-10cm triangle.
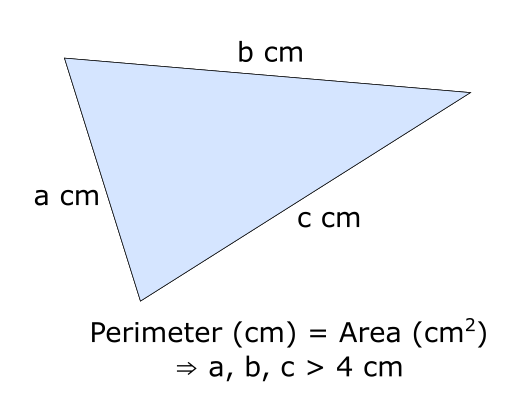
Can you show that if a triangle DOES have its perimeter in \(cm\) equal to its area in \(cm^2\), then all the edges must be longer than 4cm?
Prof. Butler's explanation is found at the twitter link in the source.
.: [GEOM], [David Butler], [New Understanding].
. . . View This Fullsize
Consider the fractions \( \dfrac{5}{29} \) and \( \dfrac{1}{2} \).
Adding tops and bottoms produces a number in between, so \( \dfrac{6}{31}\) is in between \( \dfrac{5}{29} \) and \( \dfrac{1}{2} \).
But \(\dfrac{6}{31} \) is less than half, so it must be \( \dfrac{5}{29} < \dfrac{6}{31} < \dfrac{1}{2} \).
Does adding tops and bottoms get a number in-between ... always?
.: [MS Math], [David Butler], [Number Theory].
. . . View This Fullsize
Use only the five numbers 10, 100, 1000, 10 000, 100 000,
with each appearing exactly once, and as many of +, -, ×, ÷ (and brackets) as you like, to make numbers with no zeros in their digits.

.: [MS Math], [David Butler], [Number Theory].
. . . View This Fullsize
Consider these expressions:
\( 7+8 \)
\( 8+7 \)
\( 7-8 \)
\( 8-7 \)
\( 7*8 \)
\( 8*7 \)
\( 7÷8 \)
\( 8÷7 \)
If you were to replace the \( 8 \)'s with \( 3+5 \), in which expressions would you need brackets around the \( 3+5 \)?
What if you replace \( 8 \) with \( 2*4 \), or with \( 2^3 \)?
.: [MS Math], [David Butler], [Number Theory].
. . . View This Fullsize
What do you think about this description?
Is this efficient and useful or misleadingly simplistic?
What the leading coefficient of a polynomial does to a graph:
Positive Leading coefficient => right-hand end points up
Negative Leading coefficient => right-hand end points down
Degree odd => ends point opposite ways
Degree even => ends point same way
.: [ALG2], [David Butler], [New Understanding].
. . . View This Fullsize
A polynomial with integer coefficients, as a function, produces an integer output for every integer input.
I wonder: if a polynomial as a function *does* produce an integer output for every integer input, *must* its coefficients be integers?
.: [PRE-CALC], [David Butler], [Number Theory].
. . . View This Fullsize
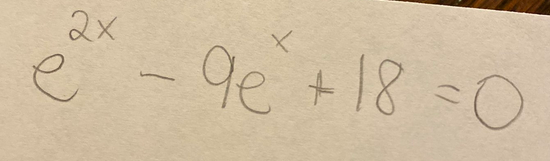
To which David Butler added:
May I please add one thing, for the purposes of helping your student with future problems?
It might be very important to consider what happens for similar equations, such as THESE two:
\(e^{2x} + 9e^x + 18 = 0\)
\(e^{2x} + 9e^x - 10 = 0\)
.: [PRE-CALC], [David Butler], [Notice, Wonder].
. . . View This Fullsize
Trace the edge of the Serpinski Figure below with one continuous line, without going over any line twice.

.: [LOGIC], [David Butler], [Geometry Snacks].