Math Arguments
Problems, Questions, and Puzzles to spark discussion and argument in the maths classroom.
Perimeter and Area
Some triangles have the same perimeter in \(cm\) as area in \(cm^2\), like the 6cm-8cm-10cm triangle.
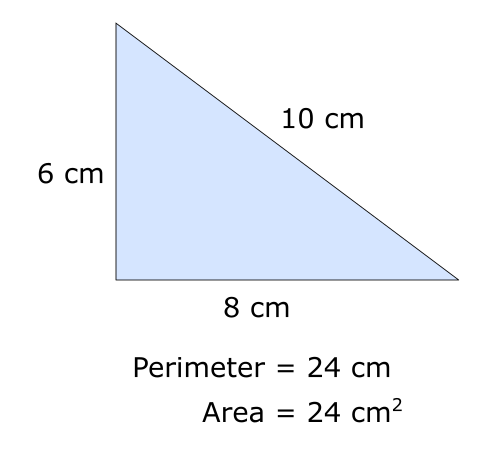
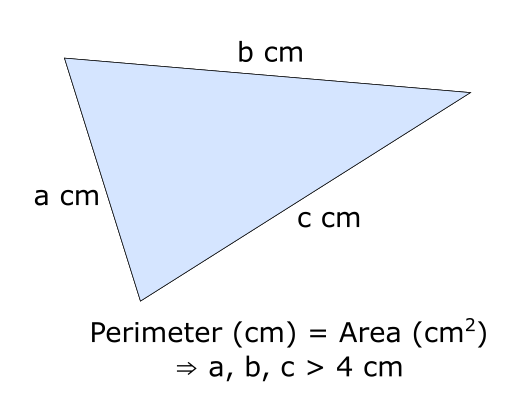
Can you show that if a triangle DOES have its perimeter in \(cm\) equal to its area in \(cm^2\), then all the edges must be longer than 4cm?
Prof. Butler's explanation is found at the twitter link in the source.
.
Source:
David Butler
Some triangles have the same perimeter in cm as area in cm^2, like the 6cm-8cm-10cm triangle. A cool fact: If a triangle DOES have its perimeter in cm equal to its area in cm^2, then all the edges must be longer than 4cm. (Thanks @edsouthall! Your problem helped me find this.)
— David Butler (@DavidKButlerUoA) July 20, 2020
More Information:
 ++
++