12 of 24 Items .... Type: Which Would You Choose?
Problems, Questions, and Puzzles to spark discussion and argument in the maths classroom.
Navigation:
- by Source
- by Course
.... - Problem Type: 101 Things
3ACT
ASN
ChatGPT
Combinatorics
Comparisons
Constructions
Create a Problem
DebateMath
Definitions
DESMOS Art
Desmos Challenge
DoThis
Epiphany
Equity
Explainer
Find the Error
Find the Pattern
Game
Geometry Snacks
Graphicacy
Graphical Approach
How Many Ways?
How Many?
Illusion
Impossible Problem
MathArt
MathStrategy
MathTip
Meme
Mimizu
Modeling
New
New Understanding
Notation
Notice, Wonder
Number Theory
Number_Search
Number_Talks
Open Middle
Optimization
Pedagogy
Policy
Proof Without Words
Puzzle
Rates
Ratios & Proportions
Raw Pure Math
Regressions
Sensible?
Sidewalk Chalk
Smart Substitution
Starters
Strategy
Terminology
The Hook
The RealWorld
Topology
Understandings
VennWords
Wait. Really?
WCYDWT
What If
What is This?
What Questions
Which Would You Choose?
WODB
Yohaku
. . . View This Fullsize
You are asked to find the roots and factors of the following polynomial function:
\( f(x) = x^4 - 2x^3 - 18x^2 + 6x + 45 \)
By the rational root theorem, possible rational roots are
\( \pm ( 1, 3, 5, 9, 15, 45 ) \).
In order to minimize your effort, you know that you should begin with the possibility that is most likely to be a root. Which roots are most likely?
.: [ALG2], [T.R.Milne], [Which Would You Choose?].
. . . View This Fullsize

What car will have the shorter path?
How could you tell for certain?
.: [GEOM], [Justin Aion], [Which Would You Choose?].
. . . View This Fullsize
So ... I've seen a couple of YouTube videos that feature songs about the Quadratic Formula. I often see it written like this:
\(x = \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}
\)
and it occurs to me that I've always written it this way:
\(x = \dfrac{-b}{2a} \pm \dfrac{\sqrt{b^2-4ac}}{2a}\)
Which one is better?
.: [ALG2], [T.R.Milne], [Which Would You Choose?].
. . . View This Fullsize
We all know that playing the middle of a tic-tac-toe game ensures that you can never lose if you play it right, but this one seems to be a bit trickier.
Where is the best place to start?
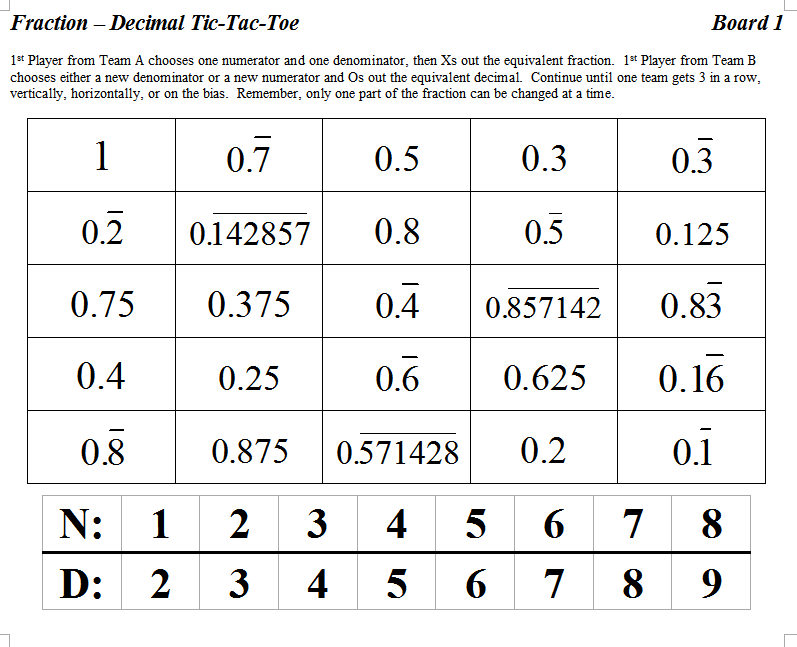
.: [MS Math], [PD], [Which Would You Choose?].
. . . View This Fullsize
What do you notice about these three equations?
\(10 * 9 * 8 * 7 \div 6 \div 5 * 4 * 3 - 2 +1 = 2015\)
\((4 * 7 * 69 ) + 83 = 2015\)
\((69 - 4) * (38 - 7) = 2015\)
Which one do you like best?
.: [ALL], [Alex Bellos], [Which Would You Choose?].
. . . View This Fullsize
Would you guess? $250,000 if correct and $100,000 if she refuses to try for it.

.: [PROBABILTY], [Curmudgeon], [Which Would You Choose?].
. . . View This Fullsize
So, students. You've had a chance to weigh in on addition and multiplication. What is the best way to do division?
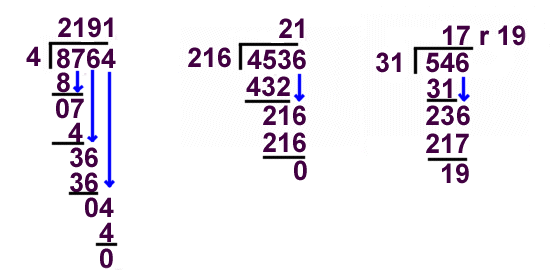
.: [MS Math], [internet], [Which Would You Choose?].
. . . View This Fullsize
A small company wants to give raises to their 5 employees. They have $10,000 available to distribute. Imagine that you are in charge of deciding how the raises should be determined.
- What are some variables you should consider?
- Describe mathematically as many different methods you can think of to distribute the raises. (We came up with nine; can you beat that?)
- What information will you need to compute those raises according to your various methods?
- Which of your methods do you feel is the most fair?
Use an atbash cipher decoder: http://rumkin.com/tools/cipher/atbash.php
- zm vjfzo znlfmg, gdl gslfhzmw vzxs.
- vjfzo kvixvmgztv yzhvw lm hzozib.
- mvklgrhn: 1p, 1p, 1p, 1p, Ldmvi'h hlm: 6p.
- R'n lmv lu gsv vnkolbvvh: 0p, 0p, 0p, 0p, nv: 10p
- kilwfxgrergb tlzoh: 1p, 1p, 2p, 2p, 4p
- olggvib, zoo li mlgsrmt.
- olggvib, 0p, 1p, 2p, 3p, 4p.
- zokszyvgrxzo liwvi, 0p, 1p, 2p, 3p, 4p.
- vnkolbvv'h xsrow'h gvhg hxlivh rm gsv olxzo hxsllo ... ru gsviv'h ml rnkilevnvmg, ml ylmfh.
.: [ALL], [Illustrative Math], [Which Would You Choose?].
. . . View This Fullsize
Which would you press ... and why?
.: [PROBABILTY], [internet], [Which Would You Choose?].
. . . View This Fullsize
This system of equations has a peculiar characteristic ... I think it is easier to solve it by analytical means than by using Desmos or a TI-84.
Do you agree?
What about it makes a graphical solution difficult?
.: [ALG1], [T.R.Milne], [Which Would You Choose?].
. . . View This Fullsize
What method works best to find the area of the triangle created by these three lines?
Organized list (a la excel)
Substitution?
Linear Combination?
Plug and Pray?
.: [ALG1], [T.R.Milne], [Which Would You Choose?].
. . . View This Fullsize
"The sum of two positive integers is 216. The greatest common factor of the two numbers is 24. What are all the possible pairs of numbers?"
What approach seems the easiest here?
I can see using solution methods such as:
- algebra
- guess and check
- organized list
- visual representation
Which (or which other) method rings true for you? Which of the two sentences eliminates the most numbers?
.: [ALG1], [David Marain], [Which Would You Choose?].
