11 of 11 Items .... Course: SAT
Problems, Questions, and Puzzles to spark discussion and argument in the maths classroom.
. . . View This Fullsize
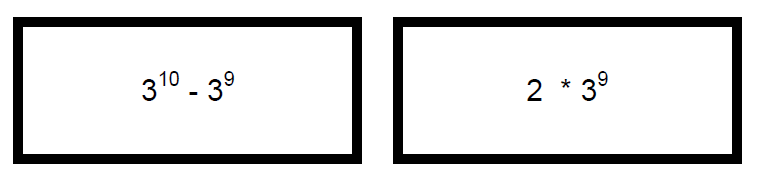
Which is true?
Left side is larger than Right side
Right Side is larger than Left Side.
The two sides are equal.
Not enough information?
How can we deal with this WITHOUT a calculator?
.: [SAT], [Curmudgeon], [Comparisons].
. . . View This Fullsize
Which mental path do you think is easiest for beginning students? (Analytical, numerical, graphical, algebraic?) Would you give a different hint to beginning students than to advanced students?
Will the average of \( 2^{48} \) & \( 2^{50}\) be less than, greater than, or equal to \( 2^{49} \)?
Can you find the actual average? (without a calculator!)
.: [SAT], [David Marain], [Number Theory].
. . . View This Fullsize
This is from the end of a section of an SAT test, and is therefore a bitch to solve. At least, the results from the test seem to indicate so. On a 5-choice multiple choice question, only 8% of respondents got this one right ... if they had covered their eyes, refused to read the question, and randomly guessed, they would have more than doubled their chances of getting it right. We can do better than that!
What numbers should I plug into the equations to test for correctness?
25. A watch loses x minutes every y hours. At this rate, how many hours will the watch lose in 1 week?
- \(7xy\)
- \(\dfrac{7x}{y}\)
- \(\dfrac{x}{7y}\)
- \(\dfrac{14y}{5x}\)
- \(\dfrac{14x}{5y}\)
.: [SAT], [SAT], [Smart Substitution].
. . . View This Fullsize
As we all know, the questions in an SAT test get harder as you get to the end of a section. I warn my students repeatedly that, as they approach the end of a section,
"If you can't see what all those people thought was the obvious answer ...You see, the question at the end aren't really difficult usually. They can be badly worded but they're rarely HARD. They are usually four-step problems that everyone else is so sure about, and the answer is so obvious that they get suckered in. These two were rated the same level of difficulty, and were answered correctly by about 3%-5% of the students.
and clearly see why that obvious answer is wrong, ...
then you are one of those who will jump to the wrong conclusion and you'll get it wrong, too."
Which one is harder?
25. A woman drives to work each day at an average speed of 40 miles per hour and returns along the same route at 30 miles per hour. If her total traveling time was 1 hour, what was the total number of miles in the trip?
- 30
- \(30\dfrac{1}{7}\)
- \(34\dfrac{2}{7}\)
- 35
- 40
24. A 25 foot ladder is placed against a vertical wall of a building with the bottom of the ladder standing on concrete 7 feet from the base of the building. If the top of the ladder slips down 4 feet, then the bottom of the ladder will slide out.
- 4ft
- 5ft
- 6ft
- 7ft
- 8ft
In each case, can you say why the obvious answer is wrong?
.: [SAT], [T.R.Milne], [Understandings].
. . . View This Fullsize
Make similar questions ...
If \(x^2+y^2 = 196\) and \((x-y)^2 = 36\), what is the value of \(xy\)?
- -116
- -80
- -8
- 80
- 160
.: [SAT], [SAT], [Epiphany].
. . . View This Fullsize
The really difficult questions on the SAT (the ones at the end of each section) are often not really that difficult -- they just seem to be hard to answer because they're hard to read and understand because of the formal mathematical writing style and the complexity of the sentence. Often the best tactic is to plug in some numbers for the vague-sounding variables and make the problem more concrete.
If the sum of these four prime numbers is a prime number greater than 20, what is the least possible value for k?"
So what can we do with this one to make it simpler to understand the question?
Where would you start?
.: [SAT], [T.R.Milne], [Notice, Wonder].
. . . View This Fullsize
If you're a junior or senior, you've seen versions of this problem before, perhaps on the SAT (the source of this problem). As I've said before, the SAT is designed in a way that calculators are not necessary and each question must be solvable in less than a minute. Often, the student is expected to change the form of the question: text to algebra, or algebra to visual (graphical); or rearrange the terms, or work backwards from the known.
The sum of the positive odd integers less than 200 is subtracted from the sum of the positive even integers less than or equal to 200. What is the resulting difference?
As it stands, that question would take you far too long to find an answer for, so it must have a simplification somewhere. What can we do to make this quicker to answer? Or simpler to understand? How can we change it?
.: [SAT], [SAT], [Epiphany].
. . . View This Fullsize

Town A is 300 km from Town B and Town B is 200 km away from Town C.
- What is the closest A and C could be?
- How far apart could they be, if they were as far apart as possible?
- How many integer distances between A&C are possible?
.: [SAT], [David Marain], [Epiphany].
. . . View This Fullsize
We have this "hard" SAT question:
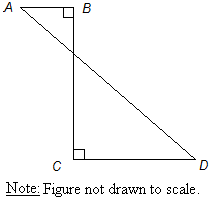
How could we redraw this to make it simpler to see and understand the solution?
.: [SAT], [internet], [Notice, Wonder].
. . . View This Fullsize

This is an actual SAT question, from later in a section so it is one that a lot of test-takers got wrong because it was a hard question, was worded strangely, had too many undefined letters, or was near the end of a section and the test-takers simply ran out of time.
What are some of the difficulties you think most students would have with it? What are some things we could do to rewrite the question so it's more clear?
.: [SAT], [internet], [Number Theory].
. . . View This Fullsize
Warm Up for Algebra Students (SAT-Type)
Sum of the areas of two squares = 60
Sum of their perimeters = 40.
If sides of the squares are \(x\) & \(y\), \(xy=?\)
(1) Is it a good idea to test integer values first?
(2) Prob asks for \(xy\) instead of \(x\) and \(y\). Can you guess why?
.: [SAT], [David Martin], [Epiphany].