12 of 86 Items .... Course: PRE-CALC
Problems, Questions, and Puzzles to spark discussion and argument in the maths classroom.
. . . View This Fullsize
If we stipulate that
\( (x+12)^2+(y+4)^2+(z+3)^2=0\), then
\( \sqrt{x^2+y^2+z^2}=?\)
Should we brute-force this or is there a more beautiful or subtle way of getting what we want?
.: [PRE-CALC], [David Marain], [Raw Pure Math].
. . . View This Fullsize
Go to this page at Desmos, and hit play. Explain what you see and why it is behaving that way.

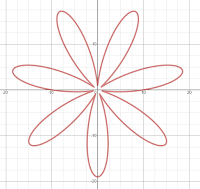
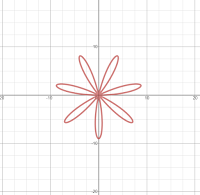
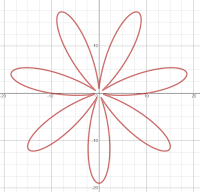
There is obvious symmetry in the figure at each value of a but should we be defining something new to describe the sequence of images? A dynamic symmetry, of sorts?
.: [PRE-CALC], [Curmudgeon], [Notice, Wonder].
. . . View This Fullsize
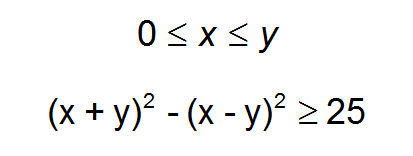
Is there enough information to determine the least possible value of y?
.: [PRE-CALC], [SAT], [Raw Pure Math].
. . . View This Fullsize
That takes care of four letters.

twenty-two to go ....
.: [PRE-CALC], [internet], [DESMOS Art].
. . . View This Fullsize
For the following functions, think about "How to graph like a math teacher."
Math teachers want to sketch graphs quickly and efficiently and choose
values of x that work "nicely" in the equation and generate integer
values of y, thus making it easier to graph.
Which points in the graph:
- are best found by inspection?
- are best found by substitution?
- are best found by symmetry?
\(y = {sin(\theta)}^2\)
\(y = sin^{-1}(\theta)\)
\(r = 3sin(3\theta)\)
What are your favorite examples of this?
.: [PRE-CALC], [T.R.Milne], [Smart Substitution].
. . . View This Fullsize
For the following functions, think about "How to graph like a math teacher." Math teachers want to sketch graphs quickly and efficiently and choose values of x that work "nicely" in the equation and generate integer values of y, thus making it easier to graph.
Which points in the graph
- are best found by inspection?
- are best found by substitution?
- are best found by symmetry?
\(x^2+y^2=25\)
\(\dfrac{(x-1)^2}{9}+\dfrac{(y+2)^2}{16} = 1\)
\(\dfrac{(x-4)^2}{9}-\dfrac{(y-4)^2}{16} = 1\)
What are your favorite examples of this?
.: [PRE-CALC], [T.R.Milne], [Smart Substitution].
. . . View This Fullsize
Let's examine the function g(n):
g(n) = smallest integer such that g(n)*n! is a perfect square.
How should we go about finding if there's a pattern in that?
.: [PRE-CALC], [James Tanton], [Raw Pure Math].
. . . View This Fullsize
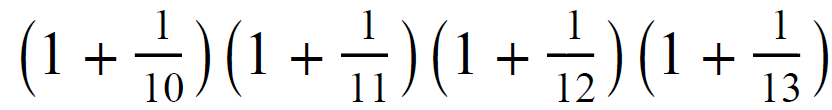
You don't need a calculator for this one either. Why not?
.: [PRE-CALC], [UVM], [Puzzle].
. . . View This Fullsize
\(log_7{\frac{1}{8}} * (log_8{25} + log_2{5}) * log_5{49} \)
Why don't we need a calculator for this problem?
.: [PRE-CALC], [UVM], [Notice, Wonder].
. . . View This Fullsize
Find two polynomials whose four points of intersection form a perfect square. (...with integer coefficients?)
What's the best way to do that?
.: [PRE-CALC], [James Tanton], [Raw Pure Math].
. . . View This Fullsize
Consider the sequence: 1, a , a2, a3, ... , an
Is the median of that sequence more than, less than, or equal to an/2 ?
What values of a could make this a dodgy question?
.: [PRE-CALC], [David Marain], [Raw Pure Math].
. . . View This Fullsize
Can you recreate these figures? Note: Unlike the previous figures, these are all "incomplete" so you will have to do two things ... (a) figure out the form of the full figure (how many pedals, etc.) and (b) restrict the domain appropriately. In Desmos, domain restriction is done this way:
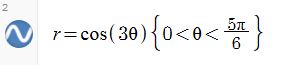
creates this:
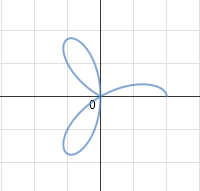
Here we go ....
3
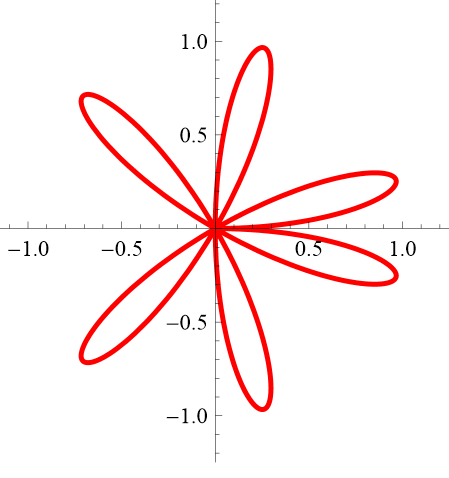
3
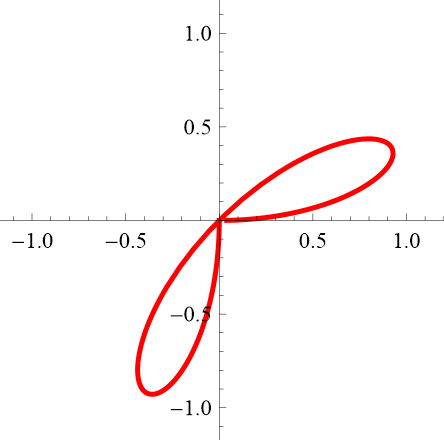
3
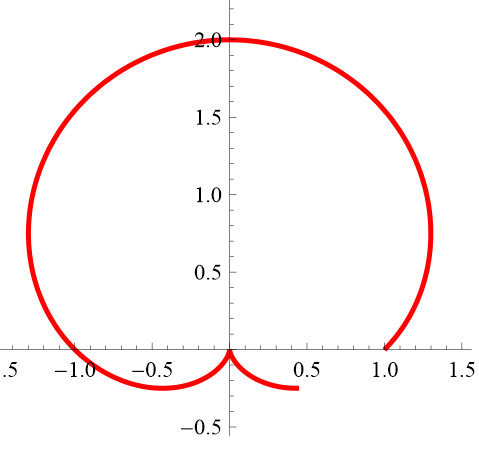
3
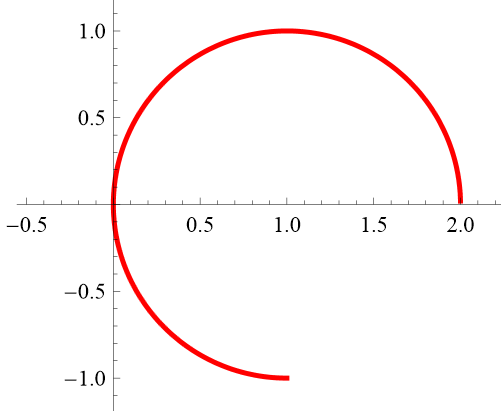
3
.: [PRE-CALC], [T.R.Milne], [DESMOS Art].