12 of 71 Items .... Course: ALG1
Problems, Questions, and Puzzles to spark discussion and argument in the maths classroom.
. . . View This Fullsize
An interesting Question ... is an algebraic method the only way to do this?
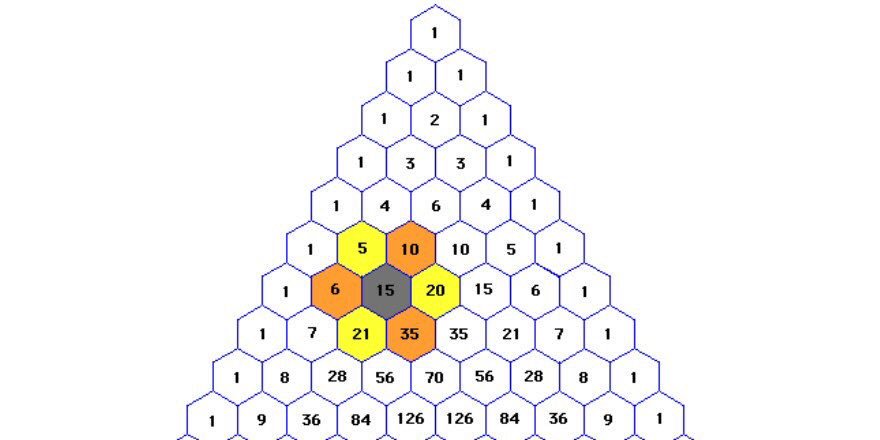
Prove that anywhere on Pascal's triangle, products of numbers in yellow and in orange are equal.
.: [ALG1], [Five Triangles], [Number Theory].
. . . View This Fullsize
We started with this:
And then we extended with: What is the fewest number of employees possible in this building?
If the ugly-sweater party was held in that factory with the minimum number of workers possible and the ratio of red to green ugly sweaters was 7:13, how likely is it that a left-handed man wore a red ugly sweater?
.: [ALG1], [m4ths], [Sensible?].
. . . View This Fullsize
We started with this:
The ratio of right-handed men to left-handed men is 7:3
The ratio of right-handed women to left-handed women is 11:1
What fraction of the factory workforce is right-handed?
But let's extend things a bit.
What is the fewest number of employees possible in this building?
.: [ALG1], [m4ths], [Ratios & Proportions].
. . . View This Fullsize
In a factory, the ratio of men to women is 2:3.
The ratio of right-handed men to left-handed men is 7:3
The ratio of right-handed women to left-handed women is 11:1
What fraction of the factory workforce is right-handed?
.: [ALG1], [m4ths], [Ratios & Proportions].
. . . View This Fullsize
It's not included in the PEMDAS Order of Operations ...
Should \(a^{b^c} = ({a^b})^c\) or should it be \(a^{b^c} = a^{(b^c)}\) ??
Does \(3^{2^0}\) equal 1 or 3?
Let's just consider easy numbers {1, 2, 3, 4} so we can explore. What's the probability that the two methods arrive at the same answer?
.: [ALG1], [Curmudgeon], [Definitions].
. . . View This Fullsize
Ask your class if there are any Pythagorean anti-Triples: \(\dfrac{1}{a^2} + \dfrac{1}{b^2} = \dfrac{1}{c^2}\) ?
If a, b, c are integers, the question seems harder, since 1/3, 1/4, 1/5 would be (to me) obvious answers - leading to the rules for Pythagorean triples and just using their reciprocals.
.: [ALG1], [James Tanton], [Epiphany].
. . . View This Fullsize
Marilyn Burns pointed out:
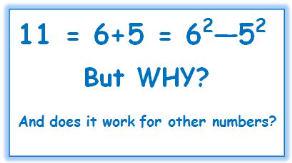
Well, does it?
Is there a pattern that always works?
.: [ALG1], [internet], [Number Theory].
. . . View This Fullsize
Take a square number and multiply by four. Is it guaranteed to still be a square number?
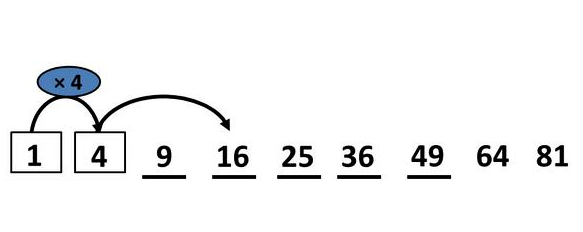
Can we generalize this rule?
Can your students explain why?
.: [ALG1], [Steve Wyborney], [Find the Pattern].
. . . View This Fullsize
The sum of \(\frac{1}{4}\) and a number is equal to the product of \(\frac{1}{4}\) and the number.
(a) Explain why the number must be negative.
(b) What's the number ?
.: [ALG1], [David Marain], [Explainer].
. . . View This Fullsize
\( x^2 = 81 \) has two solutions, -9 and 9.
But does \( \sqrt{81} \) have one solution or two?
Is it correct to say that \( \sqrt{81} \) = +9 and -9?
Or should we be saying that \( \sqrt{81} \) is an expression and that \( 9\), \(\frac{18}{2} \), \(27^{2/3} \), and \(1+6+2\), are equivalent expressions?
.: [ALG1], [Kate Nowak], [Understandings].
. . . View This Fullsize
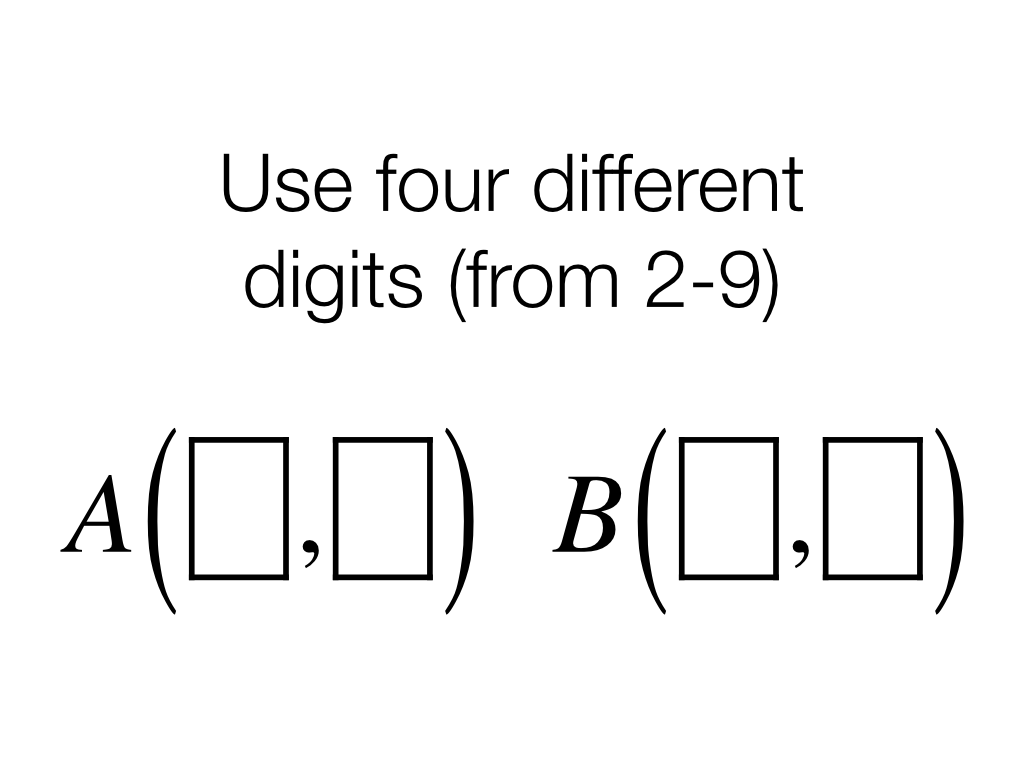
3
Challenges
- Use four different digits (from 2-9) to create two points which determine a line with the greatest possible slope.
- Use four different digits (from 2-9) to create two points which determine a line with the least possible slope.
- Use four different digits (from 2-9) to create two points which determine a line with a slope as close to zero as possible.
What does "greatest" slope mean?
What does "least" slope mean ... most negative?
.: [ALG1], [Robert Kaplinsky], [Open Middle].
